Siano dati due triangoli rettangoli simili. Se il primo ha cateti di lunghezza 3 e 4 cm, e il secondo ha area pari al quadruplo dell'area del primo, qual è la lunghezza dell'ipotenusa del secondo triangolo?
Dobbiamo tener conto di due concetti di geometria.
1) Le terne pitagoriche. Che caratterizzano i lati di alcuni triangoli rettangoli. Tra questa abbiamo quella nota 3-4-5 oltre ad altre (5-12-13, 7-24-25, ecc.). Nel nostro caso riconosciamo subito la terna 3-4-5 e conosciamo la lunghezza dell’ipotenusa senza bisogni di effettuare calcoli.
2) Il fattore di scala per lunghezze, superfici e volumi si figure geometriche simili.
Quando due figure sono simili ed hanno un fattore di scala per le lunghezze pari a f, allora per le superfici il fattore di scala sarà f 2 e per i volumi f 3.
Ad esempio due quadrati (i quadrati sono sempre simili tra loro) di lato rispettivamente 5cm e 10cm hanno un fattore di scala pari a 2. Le loro superfici di 25 cm2 e 100 cm2 hanno un fattore di scala pari a 22=4
Ugualmente due cubi di spigolo 5cm e 10cm (fattore di scala 2) avranno per facce quadrati di 25 cm2 e 100cm2 (fattore di scala pari a 22=4) e volumi di 125cm5 e 1000cm5 (fattore di scala pari a 23=8).
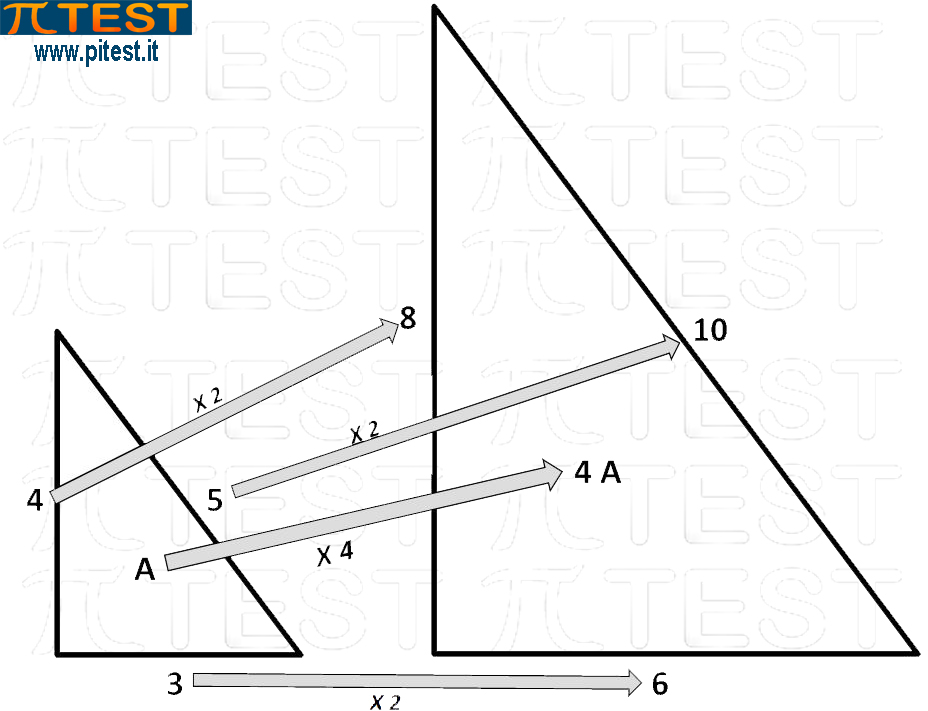
Nel testo del quiz le aree dei due triangoli rettangoli hanno con un fattore di scala per le superfici pari a 4=22 e desumiamo un fattore di scala per le lunghezze pari a 2.
Concludiamo così che il triangolo più piccolo ha una ipoteniusa di 5 cm e quello più grande ha una ipotenusa lunga il doppio, cioè 10cm.


