Questo Articolo è estratto dal Grande Manuale di logica
CONDIZIONI SUFFICIENTI
Esempio: È sufficiente che mangi troppo per far sì che digerisci male
Questa proposizione esprime la correlazione tra mangiare troppo e digerire male con una relazione di causa-effetto o implicazione.
Possiamo esprimere la stessa regola con la struttura verbale “Se… , allora… ”:
Se mangi troppo, (allora) digerisci male
Analizziamo l’affermazione con le strutture della logica proposizionale.
Poniamo:
A = mangiare troppo
B = digerire male
⇒ = implica
È sufficiente che mangi troppo per far sì che digerisci male equivale a:
|
A ⇒ B Condizione sufficiente |
ALTRI MODI DI ESPRIMERE UNA CONDIZIONE SUFFICIENTE
Oltre alle forme “è sufficiente…” e “se…, allora…” possiamo trovare anche altre espressioni che esprimono lo stesso significato logico:
|
Condizione sufficiente |
|
| Se | Se mangi troppo, (allora) digerisci male |
| Quando | Quando mangi troppo, (allora) digerisci male |
| Qualora | Qualora mangiassi troppo, (allora) digeriresti male |
| Nel caso che | Nel caso che mangi troppo, (allora) digerisci male |
| Tutte le volte che | Tutte le volte che mangi troppo, (allora) digerisci male |
| Chi | Chi mangia troppo digerisce male |
| Tutti | Tutti quelli che mangiano troppo digeriscono male |
| Gerundio | Mangiando troppo, digerisci male |
| E’ sufficiente | È sufficiente che mangi troppo per far si che digerisci male |
| Basta | Basta che mangi troppo, che digerisci male |
INDIVIDUARE LE PARTI A e B ALL’INTERNO DELLA STRUTTURA
Nella struttura verbale di un quiz quando incontriamo la particella “se” o la forma “…è sufficiente…” dobbiamo riconoscerla come PAROLA CHIAVE che ci permette di riconoscere una condizione sufficiente.
In un quiz strutturato su una condizione sufficiente dobbiamo essere in grado di individuare le due parti A e B. È spesso utile scrivere A e B sopra il testo del quiz.
Se abbiamo la forma verbale estesa “… è sufficiente..” o “…basta…” allora individuiamo “A” come soggetto del verbo “è sufficiente” o “basta” e “B” come proposizione effetto/conseguenza.
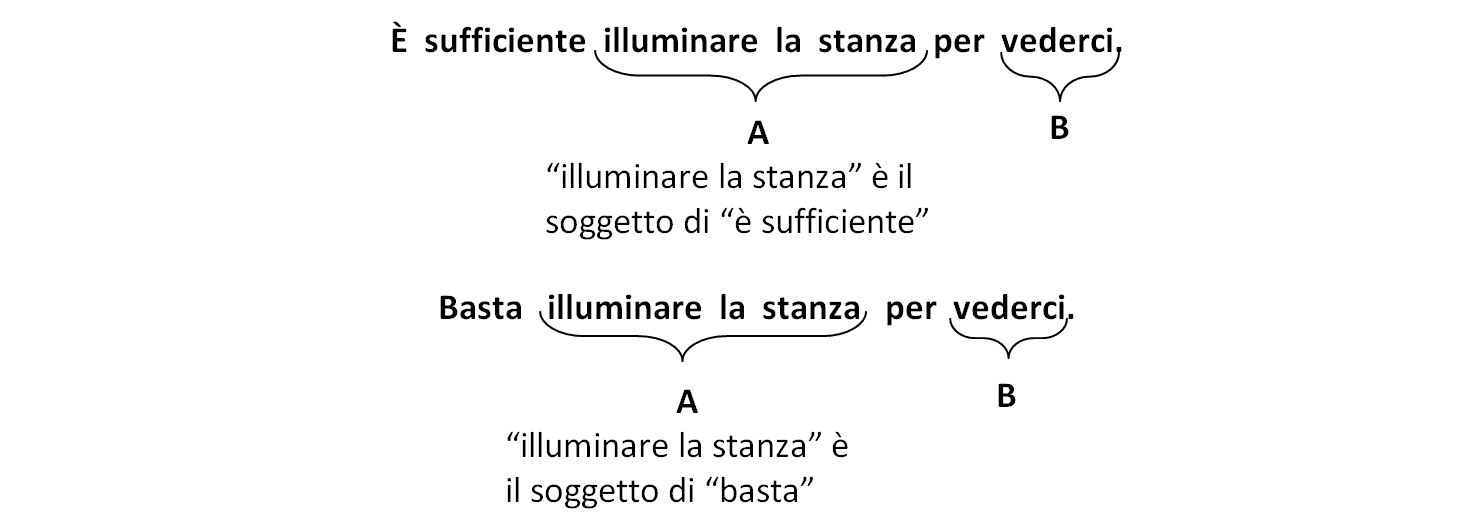
Se abbiamo la forma verbale “se…, allora…”, individuiamo “A” come parte che segue “se” e “B” come parte che segue “allora” (a volte è sottinteso).
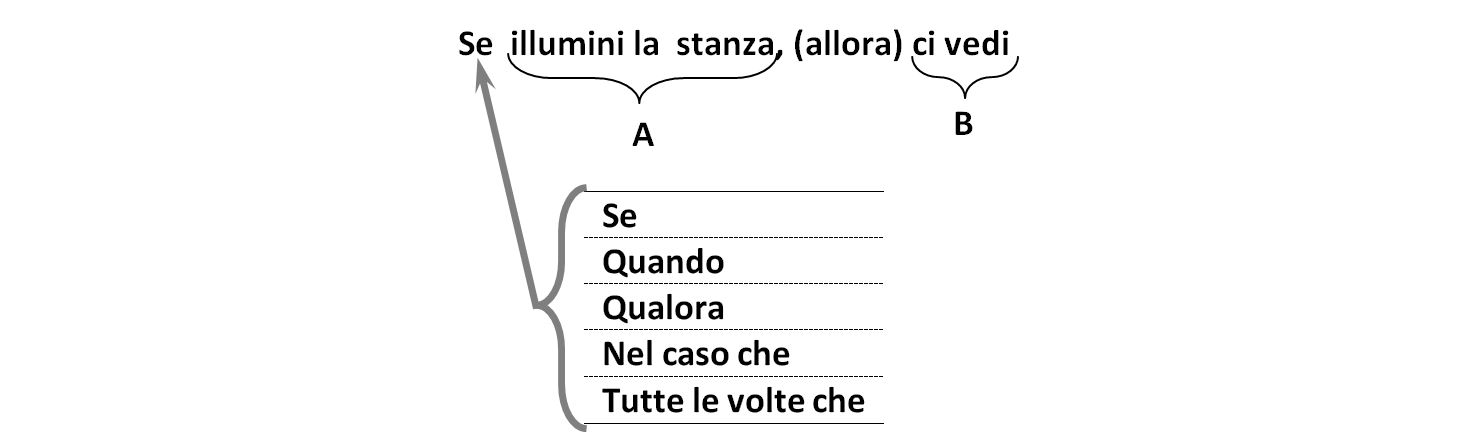
Se abbiamo la forma verbale “chi… …” , basta parafrasare nella forma “se…, allora…” e poi procedere come sopra.
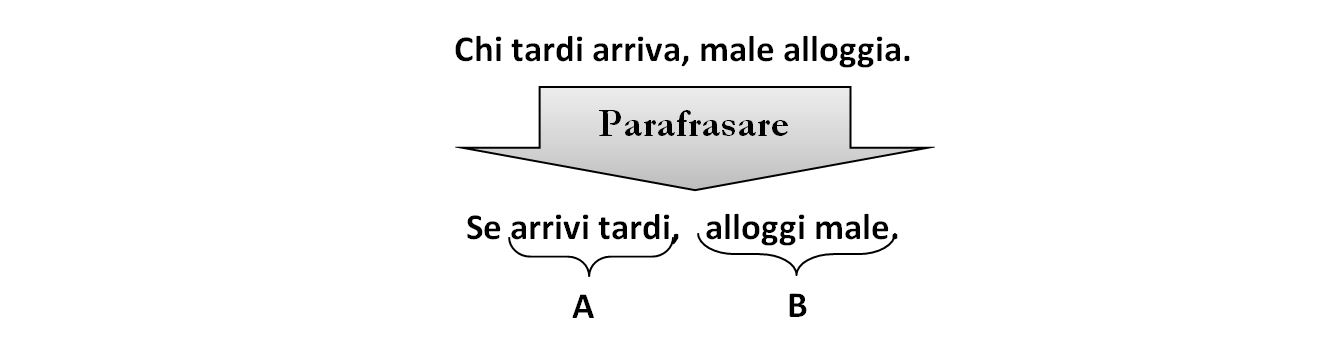
REGOLA + CASO ➔ CONCLUSIONE
Alla REGOLA di condizione sufficiente si associa un CASO. Da questa associazione possiamo trarre una conclusione.
Abbiamo quattro possibili situazioni per formulare il CASO: A, ¬A, B, ¬B.
– – [ Ruotare il cellulare per visualizzare la tabella ] – –
| REGOLA | CASO | CONCLUSIONE | ||
|
Se mangi troppo, digerisci male; A ⇒ B |
1 | A | oggi hai mangiato troppo | |
| 2 | ¬A | oggi non hai mangiato troppo | ||
| 3 | B | oggi hai digerito male | ||
| 4 | ¬B | oggi non hai digerito male | ||
Analizziamo i quattro casi. Vediamo prima i casi 1 e 4 che danno luogo a conclusioni deducibili certe. Vedremo poi i casi 2 e 3 che invece non permettono una deduzione certa.
CASO 1
È evidente che questa è una situazione molto semplice. Si percepisce con facilità che il caso (oggi hai mangiato troppo) ricade perfettamente nella applicazione della regola e la conclusione è immediata: “quindi oggi certamente digerisci male”.
– – [ Ruotare il cellulare per visualizzare la tabella ] – –
| REGOLA | CASO | CONCLUSIONE |
| Se mangi troppo, digerisci male; | oggi hai mangiato troppo; | quindi oggi digerisci male. |
| A ⇒ B | A | → B |
| ( A ⇒ B ) ᴧ A → B | ||
Questa figura logica è stata chiamata MODUS PONENDO PONENS o più semplicemente MODUS PONENS dalla scuola di pensiero stoica fiorita ad Atene nel III secolo a.C. con il filosofo Crisippo si Tarso. Questa forma di pensiero, iniseme al seguente Modus Tollens, venne classificata come “anapodittica“, ovvero senza possibilità di dimostrazione a partire da altre verità.
Il senso è il seguente:
<< Data la regola A⇒B, ponendo la verità di A allora pongo vero anche B >>
È una figura logica semplice e fin troppo evidente. Raramente viene usata in un quiz per individuare la corretta deduzione.
CASO 4
Rispetto alla precedente questa è una situazione meno semplice. Il caso (oggi non hai digerito male) ricade nella applicazione della regola e la conclusione è immediata: “quindi oggi certamente non hai mangiato troppo”.
– – [ Ruotare il cellulare per visualizzare la tabella ] – –
| REGOLA | CASO | CONCLUSIONE |
| Se mangi troppo, digerisci male; | oggi non hai digerito male; | quindi oggi non hai mangiato troppo. |
| A ⇒ B | ¬B | → ¬A |
| ( A ⇒ B ) ᴧ ¬B → ¬A | ||
Questa figura logica è stata chiamata MODUS TOLLENDO TOLLENS o più semplicemente MODUS TOLLENS dalla scuola di pensiero stoica.
Il senso è il seguente:
<< Data la regola A⇒B, togliendo la verità di B allora togliamo anche la verità di A >>
È una figura logica molto importante nei quiz dei test di ammissione. Viene spesso usata nei quiz basati sulle condizioni sufficienti.
Il concetto è che se non si manifesta l’effetto (B) allora non si sono verificate nemmeno le cause che lo producono (tra esse va considerata anche A).
CASO 2
Questa è una situazione che non porta ad una conclusione certa. Infatti la regola esprime cosa accade nel caso che “mangi troppo”, ma nulla dice nel caso che “non mangi troppo”. Non possiamo affermare né che “digerisci male”, né che “non digerisci male“.
– – [ Ruotare il cellulare per visualizzare la tabella ] – –
| REGOLA | CASO | CONCLUSIONE |
| Se mangi troppo, digerisci male; | oggi hai mangiato troppo; | quindi … ? → … ? |
| A ⇒ B | ¬A | → ? |
| ( A ⇒ B ) ᴧ ¬A → |
B (è possibile ma non certo) | |
| ¬B (è possibile ma non certo) | ||
Questa situazione viene utilizzata nei quiz come distrattore. Con una prima superficiale lettura potrebbe sembrare corretto dire che la conclusione di questo caso sia ¬B cioè che “non digerisci male”. Ma questo è un classico errore. Infatti basta ragionare che potresti “digerire male” per altri motivi; ad esempio per una congestione per la quale si digerisce male indipendentemente da quanto si è mangiato.
CASO 3
Questa è una situazione che non porta ad una conclusione certa. Infatti la regola dichiara che B accade come conseguenza di A. Ma non dice che B è generato soltanto da A. Potresti aver digerito male anche per altri motivi, ad esempio per una congestione, senza aver mangiato troppo.
– – [ Ruotare il cellulare per visualizzare la tabella ] – –
| REGOLA | CASO | CONCLUSIONE |
| Se mangi troppo, digerisci male; | oggi hai digerito male; | quindi … ? → … ? |
| A ⇒ B | B | → ? |
| ( A ⇒ B ) ᴧ B → |
A (è possibile ma non certo) | |
| ¬A (è possibile ma non certo) | ||
Questa situazione viene utilizzata nei quiz come distrattore. Con una prima superficiale lettura potrebbe sembrare corretto dire che la conclusione di questo caso sia A cioè che “hai mangiato troppo”. Ma questo è un classico errore perché possono esistere altre cause come ad esempio una congestione.
SINTESI DEI CASI ESAMINATI
– – [ Ruotare il cellulare per visualizzare la tabella ] – –
|
1 |
( A ⇒ B ) ᴧ A ➔ B | Se mangi troppo, digerisci male e oggi hai mangiato troppo, quindi oggi hai digerito male
Modus «Ponens» ovvero «Ponendo ponens» Cioè: ponendo la verità di A la pongo anche di B |
|
2 |
B (è possibile ma non certo) ( A ⇒B ) ᴧ ¬A ➔ ??? ¬B (è possibile ma non certo) |
Se mangi troppo, digerisci male e oggi non hai mangiato troppo,
… non c’è una conclusione certa |
|
3 |
A (è possibile ma non certo) ( A ⇒B ) ᴧ B ➔ ??? ¬A (è possibile ma non certo) |
Se mangi troppo, digerisci male e oggi hai digerito male,
… non c’è una conclusione certa |
|
4 |
( A ⇒ B ) ᴧ ¬B ➔ ¬A | Se mangi troppo, digerisci male e oggi non hai digerito male, quindi oggi non hai mangiato troppo
Modus «Tollens» ovvero «Tollendo tollens» Cioè: togliendo la verità di B la tolgo anche di A |
| Quiz condizioni sufficienti |
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito
