POSSIBILI RELAZIONI TRA INSIEMI
INCLUSIONE
Valutiamo la proposizione “Tutti i libri di filosofia sono difficili”.
Procediamo per passi:
1) Individuiamo i due insiemi in gioco: “libri difficili” e “libri di filosofia”. 2) Troviamo la regola relazionale tra i due insiemi: La proposizione contiene il quantificatore Tutti che rende l’affermazione valida per ogni libro di filosofia. Perciò dovremo inserire l’insieme “libri di filosofia” completamente all’interno dell’insieme dei “libri difficili”. Questa è una relazione di INCLUSIONE.
2) Troviamo la regola relazionale tra i due insiemi: La proposizione contiene il quantificatore Tutti che rende l’affermazione valida per ogni libro di filosofia. Perciò dovremo inserire l’insieme “libri di filosofia” completamente all’interno dell’insieme dei “libri difficili”. Questa è una relazione di INCLUSIONE. 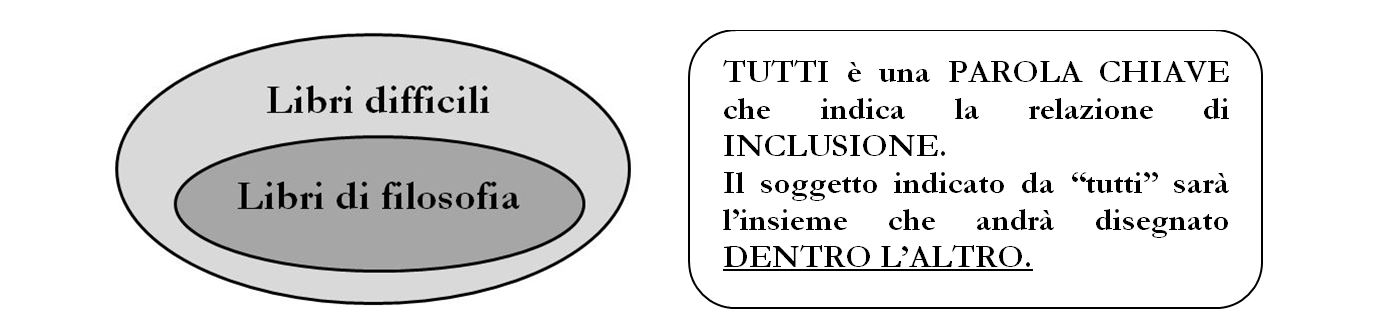 Per identificare una relazione di INCLUSIONE è valido un qualsiasi QUANTIFICATORE AFFERMATIVO UNIVERSALE O ASSOLUTO:
Per identificare una relazione di INCLUSIONE è valido un qualsiasi QUANTIFICATORE AFFERMATIVO UNIVERSALE O ASSOLUTO:
| QUANTIFICATORI UNIVERSALI O ASSOLUTI | |
| AFFERMATIVI | |
| Tutti | Tutti gli uomini sono mortali |
| Ogni | Ogni uomo è mortale |
| Ognuno | Ognuno di voi è ricco. |
| Ciascuno | Ciascuno di voi è capace. |
| Chiunque | Chiunque arriva sarà interrogato |
| Chi è…. | Chi è romano è italiano = Tutti i romani sono italiani |
| Sottinteso | I gatti sono affettuosi = Tutti i gatti sono affettuosi |
| Continua la lettura …→ |
||
| Possibili relazioni tra diversi insiemi | ||
| Inclusione | Esclusione | Intersezione o inclusione parziale |
| Esclusione parziale | Doppia inclusione | Insieme complemetare |
| Quiz sulle relazioni tra diversi insiemi | ||
| Quiz 1 |
Quiz 2 |
|
| Quiz sul corretto completamento di un sillogismo |
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito


