PROBLEMI DI PRODUZIONE
LAVORATORI CON LO STESSO RITMO DI LAVORO
Impariamo a gestire i dati dei quiz in una tabella a tre colonne nelle quali collochiamo le tre variabili del problema: numero di lavoratori, quantità di prodotto e tempo impiegato.
Il quesito presenta una situazione iniziale. Metteremo i dati relativi a questa situazione nella prima riga. I lavoratori possiedono tutti la stessa capacità produttiva. Su una nuova situazione, che è una modifica di quella iniziale viene richiesto di calcolare il valore corrispondente ad uno delle tre variabili. Vediamo come possiamo facilmente applicare criteri di proporzionalità diretta o inversa per mettere in relazione le grandezze.
Abbiamo tre possibili situazioni:
1) Quando il numero di lavoratori è lo stesso, all’aumentare del tempo aumenta anche la produzione. Il legame tra prodotto e tempo è di proporzionalità diretta.
Ad esempio:
Tre falegnami che possiedono lo stesso ritmo di lavoro producono 9 tavoli in 8 ore di lavoro. Quanti tavoli potrebbero produrre i tre falegnami se lavorassero per 24 ore?
Mettiamo i dati del quiz nella tabella:
Per la proporzionalità diretta abbiamo:
9 : X = 8 : 24
X = (9 • 24) / 8 = 27
Possiamo giungere allo stesso risultato con questo ragionamento: se il tempo triplica (da 8 a 24 c’è un fattore x3), allora, per la proporzionalità diretta, triplica anche il prodotto e perciò avremo 9 • 3 = 27.
2) Quando il tempo di produzione è lo stesso, all’aumentare del numero di lavoratori aumenta anche la produzione. Il legame tra lavoratori e prodotto è di proporzionalità diretta.
Ad esempio:
Cinque falegnami che possiedono lo stesso ritmo di lavoro producono 8 tavoli in 10 ore di lavoro. Quanti tavoli potrebbero produrre venticinque falegnami che possiedono lo stesso ritmo di lavoro se lavorassero per lo stesso tempo?
Mettiamo i dati del quiz nella tabella:
Per la proporzionalità diretta abbiamo:
5 : 25 = 8 : X
X = (25 • 8) / 5 = 40
Possiamo giungere allo stesso risultato con questo ragionamento: se il numero di lavoratori quintuplica (da 5 a 25 c’è un fattore X5), allora, per la proporzionalità diretta, quintuplica anche il prodotto e perciò avremo 8•5=40.
3) Quando la quantità di prodotto è la stessa, all’aumentare del numero di lavoratori c’è bisogno di un tempo minore di produzione. Il legame tra lavoratori e tempo è di proporzionalità inversa.
Ad esempio:
Otto falegnami che possiedono lo stesso ritmo di lavoro producono 10 tavoli in 3 ore di lavoro. Quanto tempo impiegherebbero quattro falegnami per produrre lo stesso numero di tavoli?
Mettiamo i dati del quiz nella tabella:
Per la proporzionalità inversa abbiamo:
8 : 4 = X : 3
X = (8 • 3) / 4 = 6
Possiamo giungere allo stesso risultato con questo ragionamento: se il numero di lavoratori si dimezza (da 8 a 4 c’è un fattore :2), allora, per la proporzionalità inversa, raddoppia il tempo. Avremo .
Riassumiamo le tre possibili situazioni nel seguente schema.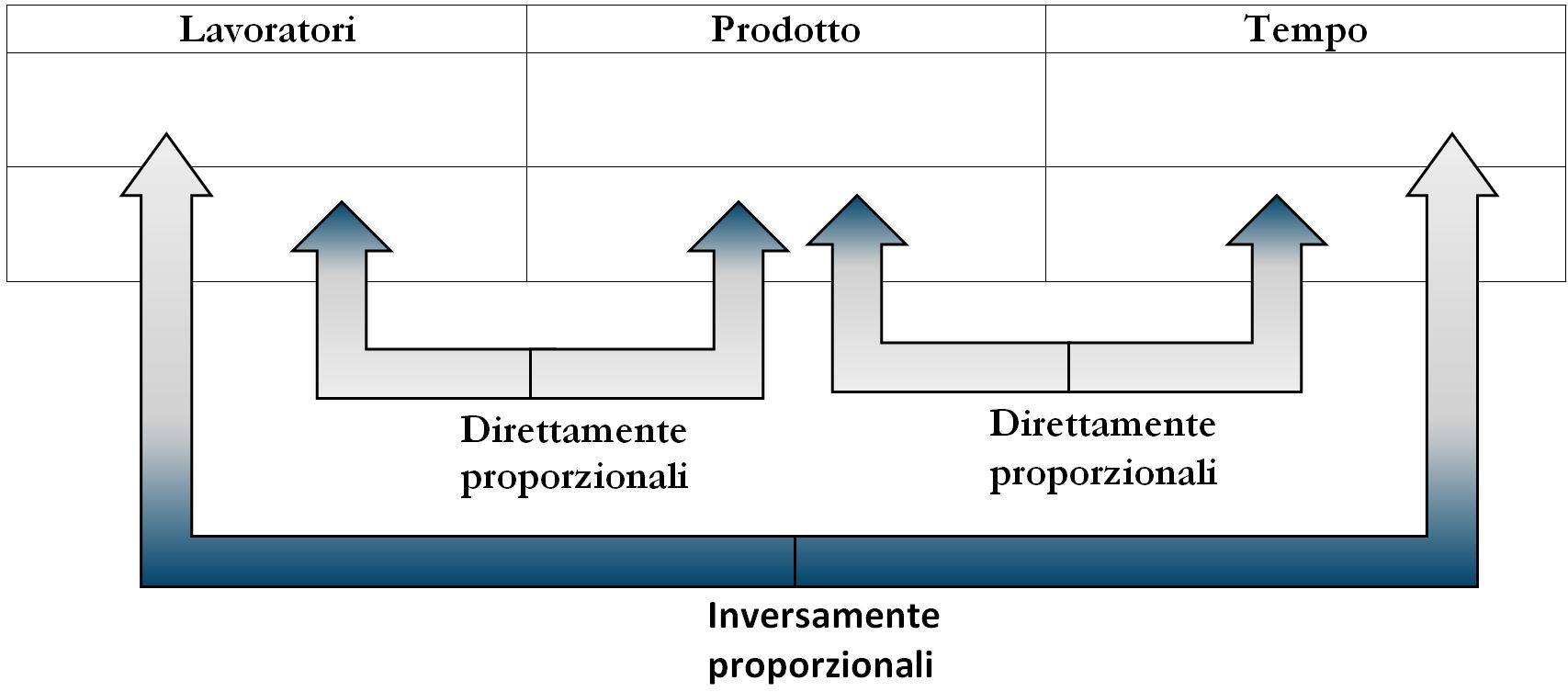
Un procedimento particolare va utilizzato quando il quiz propone una situazione con la variazione di due variabili come nel Quiz 2.
QUIZ PROBLEMI DI PRODUZIONE |
|||
|---|---|---|---|
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito
