TAVOLE DI VERITÀ
È opportuno affrontare lo studio di questo capitolo dopo aver studiato la logica proposizionale e le deduzioni (sillogismi, condizioni sufficienti e condizioni necessarie).
Le tavole di verità permettono di esprimere il valore di Vero o Falso per un certo enunciato costituito da operatori logici applicati a due proposizioni A e B.
Si inizia dalla tabella che propone tutte le combinazioni possibili tra i valori di A e B.
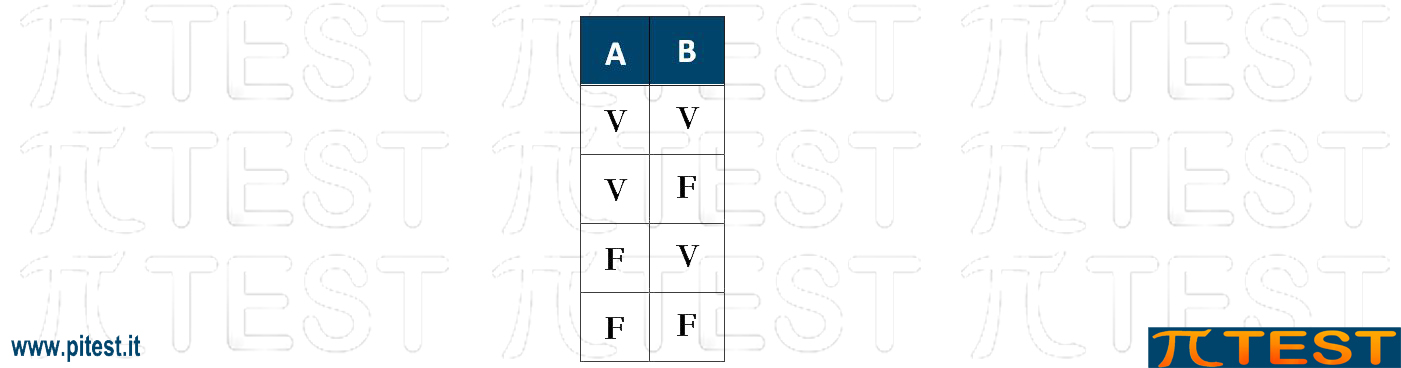
Consideriamo diverse correlazioni logiche tra A e B
LA NEGAZIONE (¬)
La negazione semplicemente inverte il senso della proposizione: da vera diventa falsa e viceversa.
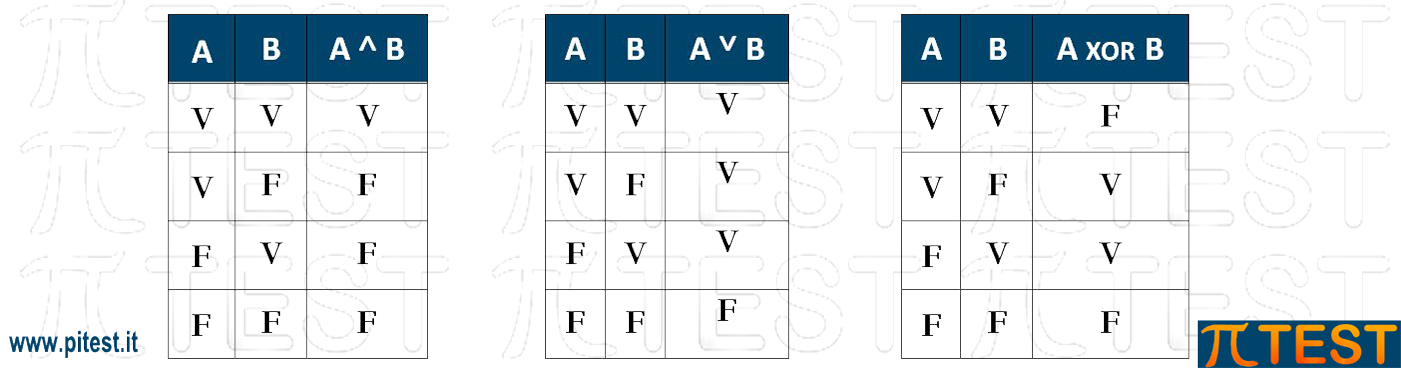
AND (˄), OR (˅) e XOR
Facciamo riferimento a quanto esposto nell’articolo di logica proposizionale sui connettivi logici e come si ritrovano nelle tavole di verità:
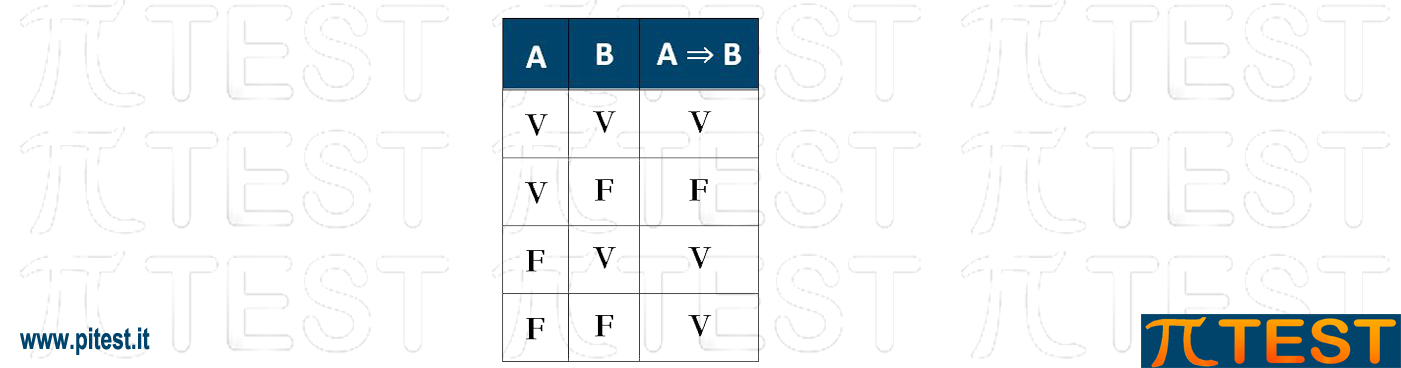
IMPLICAZIONE
Facciamo riferimento allo studio delle condizioni sufficienti. Teniamo presente la tabella di applicazione delle condizioni sufficienti con i quattro possibili casi.
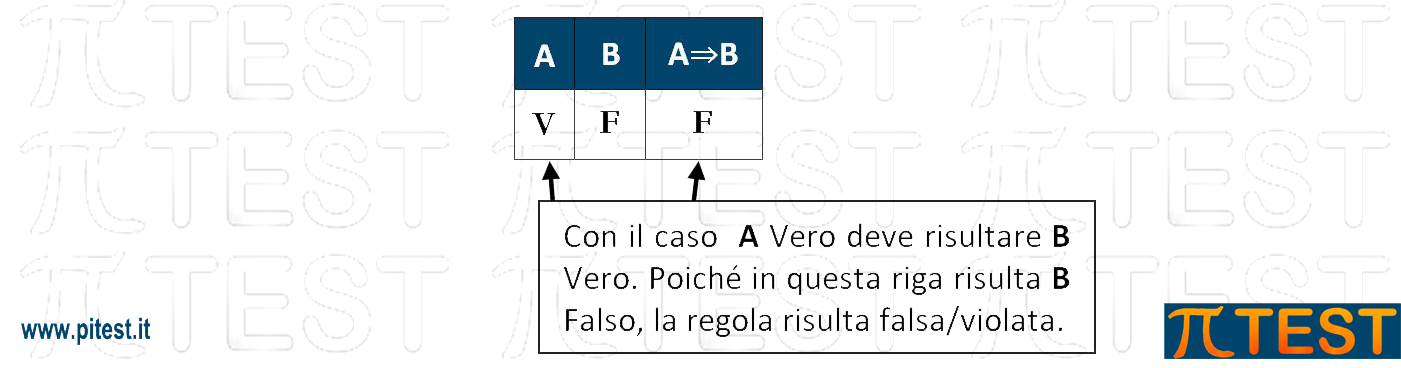
Nel “modus ponens”, data la regola A⇒B , quando si verifica il caso A (A Vero), allora sarà di conseguenza vero anche B. Quando invece si verifica il caso ¬A (A Falso), B può assumere entrambi i valori.
Nella tavola di verità nel caso A Vero e B Vero la regola è ben applicata e pertanto la regola è Vera.
Nel caso A Vero e B Falso la regola NON è ben applicata e pertanto la regola è Falsa.
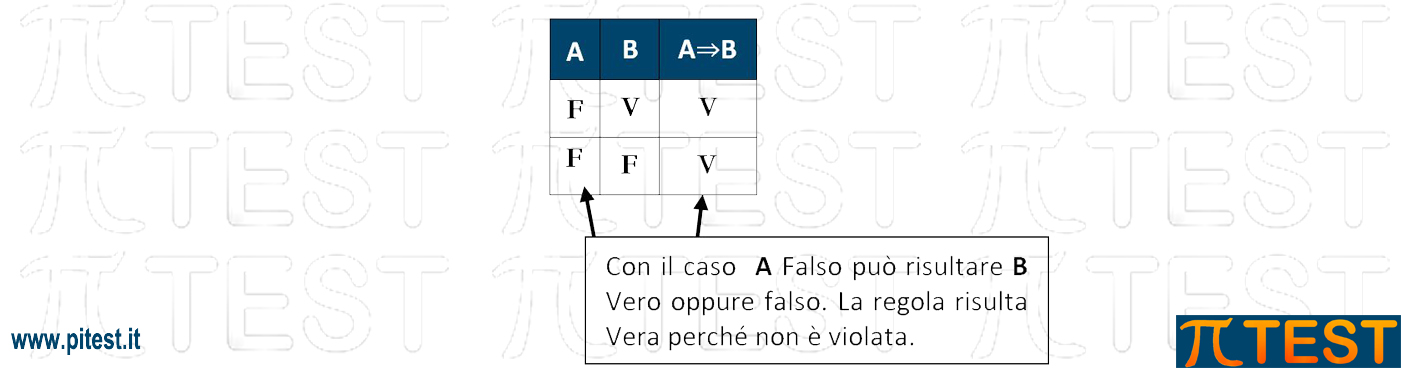
Nel caso A Falso la regola non fornisce deduzioni certe e possiamo avere liberamente B Vero oppure B Falso la regola NON è violata e pertanto è Vera.
Riassumendo:
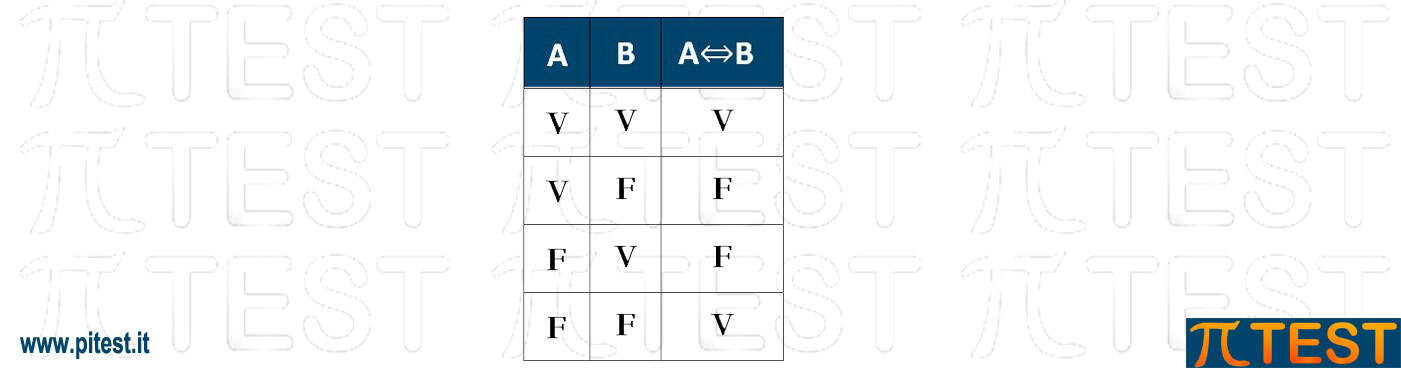
DOPPIA IMPLICAZIONE
Facciamo riferimento allo studio delle condizioni sufficienti e necessarie. Teniamo presente la tabella di applicazione con i quattro possibili casi.
Nella tabella di verità nel caso A Vero e B Vero la regola è ben applicata e pertanto la regola è Vera.
Nel caso A Vero e B Falso la regola NON è ben applicata e pertanto la regola è Falsa/violata.
Nel caso A Falso e B Vero la regola NON è ben applicata e pertanto la regola è Falsa/violata.
Nel caso A Falso e B Falso la regola è ben applicata e pertanto la regola è Vera.
Riassumendo:
| QUIZ Tavole di verità |
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito
