Negazione di connettivi logici
Esaminiamo ora l’uso del connettivo logico NOT (¬) insieme ai connettivi logici AND (˄) e OR (˅). Diciamo per semplicità “negare AND” o “negare OR”, ovvero negare una proposizione complessa.
Negazione di AND
¬ (a ˄ b)
Poniamo a = io canto e b = io ballo.
Utilizziamo il connettivo logico AND: a ˄ b io canto e io ballo.
Ora neghiamo a ˄ b e scriviamo ¬ (a ˄ b).
¬ (a ˄ b) può essere espressa verbalmente come: “Non è vero che io canto e ballo”
Ragioniamo per capire in quali situazioni risulta verificata (cioè vera) la negazione.
L’uso di AND prevede che entrambe le parti a e b siano vere. Se è falsa una o è falsa l’altra, allora stiamo negando quanto è stato espresso da AND. Cioè, se “io canto ma non ballo” oppure se “io ballo ma non canto” sto negando il fatto che “io canto e ballo”. Ovviamente la proposizione complessa a ˄ b risulta falsa, cioè negata, anche nel caso che le due proposizioni a e b siano entrambe false.
Se scriviamo questo ragionamento in modo simbolico otteniamo: ¬ (a ˄ b) = ¬ a ˅ ¬ b
Questa importante osservazione costituisce una delle due leggi di De Morgan.
|
Prima legge di De Morgan ¬ (a ˄ b) = ¬ a ˅ ¬ b |
Negazione di OR
¬ (a ˅> b)
Poniamo a = io canto e b = io ballo.
Utilizziamo il connettivo logico OR: a ˅ b io o canto o ballo.
Ora neghiamo a ˅ b e scriviamo ¬ (a ˅ b).
¬ (a ˅ b) può essere espressa verbalmente come: “Non è vero che io canto oppure ballo”
Ragioniamo per capire in quali situazioni risulta verificata (cioè vera) la negazione.
L’uso di OR prevede che almeno una delle due parti a o b sia vera. Se sono false entrambe, allora stiamo negando quanto è stato espresso da OR. Cioè, se “io non canto” e “io non ballo” sto negando il fatto che “io canto oppure ballo”.
Se scriviamo questo ragionamento in modo simbolico otteniamo: ¬(a ˅ b) = ¬a ˄ ¬b
Questa importante osservazione costituisce la seconda delle due leggi di De Morgan
|
Seconda legge di De Morgan ¬ (a ˅ b) = ¬ a ˄ ¬ b |
NEGAZIONE DI XOR
![]()
Poniamo a = io canto e b = io ballo
Utilizziamo il connettivo logico XOR: ![]() : io o solo canto o solo ballo.
: io o solo canto o solo ballo.
Ora neghiamo a XOR b e scriviamo ![]() .
.
che può essere espressa come: “Non è vero che io o solo canto o solo ballo”
Ragioniamo per capire in quali situazioni risulta verificata (cioè vera) la negazione.
L’uso di XOR prevede che una ed una sola delle due parti a o b sia vera. Se si verificano entrambe, allora stiamo negando quanto è stato espresso da XOR. Anche se non si verificano entrambe stiamo negando.
A differenza della negazione di AND e di OR la cui negazione corrisponde ad una unica legge (De Morgan), esistono infatti due situazioni possibili che negano XOR.
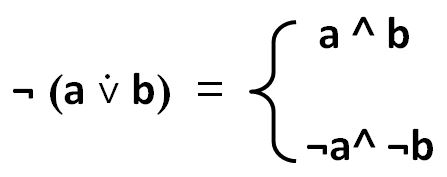
Quando un quiz coinvolge una disgiunzione esclusiva XOR, capita spesso che presenti una struttura tale da riuscire a coinvolgere nella risposta corretta entrambe le due situazioni che lo negano.
| Quiz | Quiz | Quiz |
| Negazioni Multiple | Negazioni di Connettivi Logici |
| Logica Proposizionale | Negazioni di Quantificatori |
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito


