PESATE
 |
Non sappiamo quale sia tra i tre oggetti quello più pesante e disponiamo di una bilancia a bracci.
Ci chiediamo quante pesate dobbiamo effettuare al minimo per essere certi di individuare l’oggetto più pesante. Chiamiamo i tre oggetti X, Y e Z.
Poniamo l’oggetto X su un piatto e l’oggetto Y sull’altro piatto della bilancia per comparare i loro pesi. Il terzo oggetto Z rimane fuori dalla pesata.
Possono verificarsi tre diverse situazioni. In ogni caso riusciamo ad individuare l’oggetto più pesante dei tre.
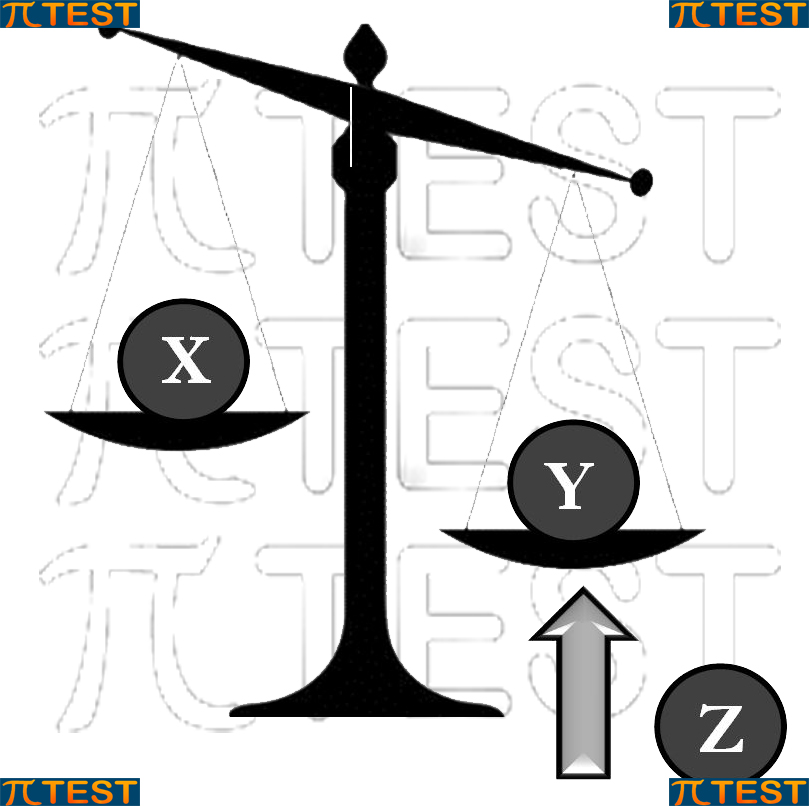
| La bilancia pende a destra. Avremo individuato a destra l’oggetto pesante. (oggetto Y) | La bilancia pende a sinistra. Avremo individuato a sinistra l’oggetto pesante. (oggetto X) | La bilancia rimane in equilibrio indicando che i due oggetti hanno peso uguale. L’oggetto più pesante sarà quello rimasto fuori dalla bilancia. (oggetto Z) |
 |
 |
 |
Il ragionamento precedente sarebbe identico se l’oggetto diverso fosse più leggero invece che più pesante degli altri due. In tal caso cambierebbe solo il risultato delle prime due situazioni.
|
|
Martina possiede 3 gettoni apparentemente identici, uno dei quali è però più pesante degli altri. Avendo a disposizione una bilancia a due piatti, quante pesate saranno sufficienti per essere certi di individuarlo?
Come abbiamo già spiegato, è sufficiente una sola pesata per individuare un oggetto più pesante degli altri due che sono identici.
Immaginiamo ora la stessa situazione con 9 oggetti identici in tutto tranne nel fatto che uno di questi pesa più degli altri 8.
Ci chiediamo quante pesate dobbiamo effettuare al minimo per essere certi di individuare l’oggetto più pesante. Chiamiamo i nove oggetti 1, 2, 3, 4, 5, 6, 7, 8, 9.
Dividiamo i 9 oggetti in 3 gruppi da 3 oggetti.
Eseguiamo sui tre gruppi la stessa tecnica precedente mettendo due gruppi sui piatti della bilancia e lasciandone uno fuori. Per lo stesso principio con una sola pesata si individua il gruppo che contiene l’oggetto più pesante.
All’interno del gruppo individuato troviamo l’oggetto più pesante con una seconda pesata eseguita con la stessa tecnica. Abbiamo visto così che avendo nove oggetti, il numero di pesate necessarie è due.
Potremmo dimostrare che con un numero di oggetti compreso tra 3 e 9 (4, 5, 6, 7 e 8) possiamo individuare l’oggetto più pesante con sole due pesate. Ad esempio con 7 oggetti possiamo creare tre gruppi contenenti 2, 2 e 3 oggetti. Confrontiamo i due gruppi da 2 oggetti. Se individuiamo uno dei due gruppi come più pesante, poi confronteremo con una seconda pesata i 2 oggetti che componevano il gruppo. Altrimenti se i due gruppi da 2 oggetti risultano uguali in peso, questo significherà che l’oggetto più pesante appartiene al terzo gruppo che non è stato pesato; questo gruppo è composto da 3 oggetti e sarà sufficiente una sola altra pesata. In sintesi con due sole pesate saremo in grado di risolvere il problema.
Consideriamo un gruppo di 27 oggetti come raggruppamento “notevole” quando la numerosità è superiore a 9. Suddividiamo i 27 oggetti in tre gruppi da 9 oggetti da confrontare con una prima pesata; sul gruppo individuato di 9 oggetti possiamo procedere come nel caso precedente con altre due pesate. In tutto basteranno tre pesate.
Per una numerosità compresa tra 9 e 27 (10, 11, … , 26) potremmo dimostrare che sono sufficienti tre pesate come nel caso di 27 oggetti.
Possiamo arrivare a determinare una regola generale per stabilire il numero minimo di pesate che fa riferimento alle potenze di 3: 31=3, 32=9, 33=27, 34=81, …
Se la numerosità degli oggetti è uguale ad una potenza di 3 come 3x, allora il numero di pesate è uguale a x, il valore dell’esponente di 3. Se la numerosità degli oggetti è diversa da una potenza di 3, allora si fa riferimento alla potenza di 3 successiva al valore della numerosità e se ne prende l’esponente. Ad esempio se abbiamo una numerosità di 22 oggetti, faremo riferimento al numero 27 (33) ed avremo che con tre sole pesate potremo individuare l’oggetto più pesante tra 22 oggetti identici in tutto tranne nel fatto che uno è più pesante degli altri.
Come abbiamo già osservato nella spiegazione del caso di tre oggetti, il ragionamento precedente sarebbe identico se l’oggetto diverso fosse più leggero invece che più pesante degli altri due.
| Numero di oggetti | Numero di pesate necessarie |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| 5 | 2 |
| ⁞ | 2 |
| 32 = 9 | 2 |
| 10 | 3 |
| 11 | 3 |
| ⁞ | 3 |
| 26 | 3 |
| 33 = 27 | 3 |
| 28 | 4 |
| 29 | 4 |
| ⁞ | 4 |
| 34 = 81 | 4 |
| ⁞ | ⁞ |
| 3n | n |
|
|
Lucia possiede 13 anelli apparentemente identici, uno dei quali è però più pesante degli altri. Avendo a disposizione una bilancia a due piatti, quante pesate saranno sufficienti per essere certi di individuarlo?
Facciamo riferimento alla tabella sovrastante. Il numero 13 è nella fascia 10-27 (33) e pertanto necessitano tre pesate.
Questo semplice ragionamento è sufficiente al fine della risposta al quiz. Non è necessario individuare quali operazioni specifiche dobbiamo effettuare.
Per chi volesse "togliersi la soddisfazione" di capire quali sono le pesate da effettuare realmente può seguire il seguente schema:
1) Dividiamo i 13 oggetti in tre gruppi da 5, 5 e 3 oggetti.
2) Mettiano sui piatti della bilancia i due gruppi di 5 oggetti. ed effettuiamo la prima pesata. Se la bilancia individua uno dei due gruppi come più pesante dell'altro proseguiamo le operazioni su questo. Se invece la bilancia risulta neutrale (i due gruppi da 5 hanno lo stesso peso) allora deduciamo che l'anello più pesante si trova nel gruppo di tre anelli rimasto fuori dalla pesata; in tale ipotesi sarà sufficiente una sola seconda pesata per individuare l'anello più pesante all'interno del gruppo di tre, ponendone uno e uno sui due piatti e lasciandone fuori uno, come abbiamo spiegato nella prima parte del presente articolo.
3) Se abbiamo individuato come più pesante un gruppo di 5 anelli, allora procediamo con una seconda pesata mettendone due e due sui due piatti e lasciandone fuori uno. Se individuiamo uno dei due gruppi di 2 anelli come più pesante concluderemo con una ultima terza pesata per confrontare i due anelli. Se invece la bilancia risulta neutrale (i due gruppi da 2 hanno lo stesso peso) allora deduciamo che l'anello più pesante e quello rimato fuori e non abbiamo bisogno di altre pesate.
Concludiamo che è possibile individuare l'anello più pesante all'interno dei 13 anelli con due o tre pesate. Poiche il quiz chede di quante pesate abbiamo bisogno per essere certi di individuare l'anello più pesante, la risposta è: tre pesate.
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito
Questo Articolo è estratto dal Grande Manuale di logica
