QUIZ CON LE CONDIZIONI SUFFICIENTI
“Se nevica, Arianna accende il camino”. Se la precedente affermazione è vera, allora è sicuramente vero che:
1) Cerchiamo la PAROLA CHIAVE:
è “Se..”. Si tratta di una condizione sufficiente.
2) Individuiamo le parti A e B della condizione sufficiente
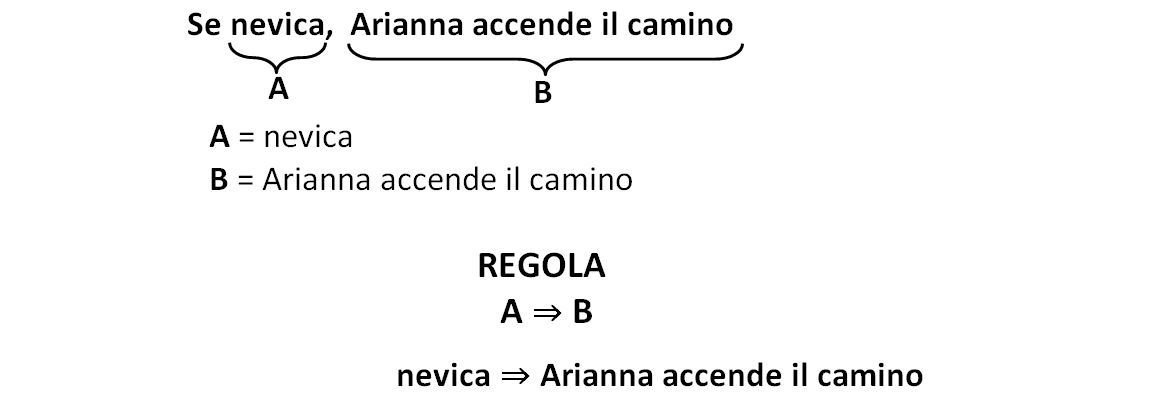
3) Analizziamo le risposte. Viene prima proposto un CASO e poi la conseguenza. Dobbiamo individuare in quale situazione la conseguenza proposta è sicuramente vera.
Nelle risposte A), B) ed E) osserviamo che il CASO viene introdotto con la forma “se..”. In questo caso la particella “se” non serve a stabilire una regola. Serve piuttosto ad introdurre il CASO. Per esempio la risposta A) va interpretata così: “poniamo il caso che Arianna accende il camino…”.
Nella risposta D) il caso viene introdotto in modo simile dalla particella “quando”. Osserviamo che in questa formulazione viene prima esposta la conclusione “Arianna non accende il camino” e poi il CASO in cui si verifica “quando c’è il sole”. Infatti la condizione sufficiente non necessariamente deve essere scritta secondo la sequenza “se A allora B”, ma può anche essere scritta “B se A”.
A) se Arianna accende il camino, vuol dire che nevica
Caso: Arianna accende il camino B
Rispetto alla tabella delle situazioni possibili ci troviamo nel CASO 3 ( A ⇒ B ) ᴧ B
Questa situazione non determina una deduzione certa, ma è possibile sia A che ¬A, cioè è possibile che nevica oppure che non nevica. Questa non è la risposta corretta che dovrebbe individuare una deduzione certa.
B) se non nevica Arianna non accende il camino
Caso: non nevica ¬A
Rispetto alla tabella delle situazioni possibili ci troviamo nel CASO 2 ( A ⇒ B ) ᴧ ¬A
Questa situazione non determina una deduzione certa, ma è possibile sia B che ¬B, cioè è possibile che Arianna accende il camino oppure che Arianna non accende il camino. Questa non è la risposta corretta che dovrebbe individuare una deduzione certa.
C) non nevica e quindi Arianna tiene spento il camino (equivalente a non accende)
Caso: non nevica ¬A
Con una differenza nella formulazione abbiamo la stessa situazione proposta nella risposta B
D) Arianna non accende il camino quando c’è il sole
Caso: c’è il sole (che equivale a non nevica) ¬A
Così come nella risposta C), anche ora abbiamo la stessa situazione proposta nella risposta B) anche se con una differente formulazione. In questa risposta il caso si trova alla fine della frase proposto con la particella "quando"
E) se Arianna non accende il camino, vuol dire che non nevica
Caso: Arianna non accende il camino ¬B
Rispetto alla tabella delle situazioni possibili ci troviamo nel CASO 4 ( A ⇒ B ) ᴧ ¬B
La deduzione conseguente deve essere “non nevica”, ¬A come proposto nella risposta E).
Abbiamo un “MODUS TOLLENS” che rappresenta una deduzione certa.
( A ⇒ B ) ᴧ ¬B ➔ ¬A
La deduzione “vuol dire che non nevica” è sicura.
Abbiamo individuato la risposta corretta.
Continua con il prossimo quiz…→
| Quiz CONDIZIONI SUFFICIENTI | Quiz CONDIZIONI NECESSARIE |
||
| Quiz 1 | Quiz 2 | Quiz 1 | Quiz 2 |
| Teoria | |||
| Condizioni sufficienti | Condizioni necessarie | ||
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito


