TEST DI AMMISSIONE A MEDICINA ED ODONTOIATRIA
Anno Accademico 2021/2022
Quiz n°56 – Fisica e Matematica
Il presente quiz non ha alcuna risposta corretta per un GRAVE errore del ministero
Medicina 2021
Se x ∈ [0, π), qual è la soluzione della disequazione?
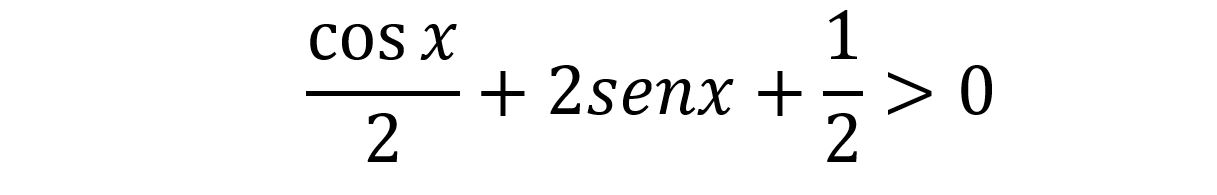
Il presente quiz non ha alcuna risposta corretta per un GRAVE errore del ministero
Segue un quiz proposto in una versione variata opportunamente in modo da avere una soluzione
Medicina 2021 - VARIATO
Se x ∈ [0, π), qual è la soluzione della disequazione?
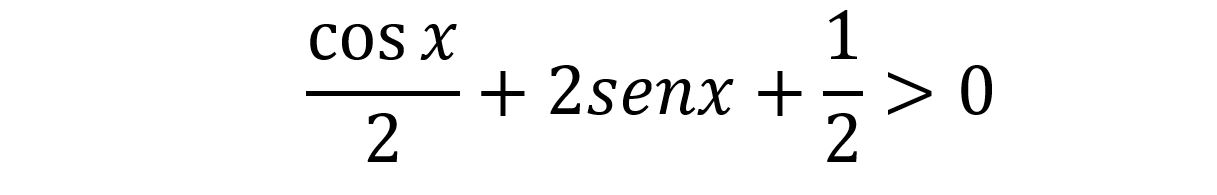
Il quiz, così come era stato formulato non aveva alcuna risposta valida. Abbiamo variato il quiz indicando l'intervallo [0, π) anziché [0, π], ovvero abbiamo escluso il punto x= π nell'intervallo di valutazione della disequazione. Vedremo come questa variazione rende valida una risposta del quiz.
Ricordiamo che le funzioni sen(x) e cos(x) nell'intervallo 0-π assumono i valori come in figura
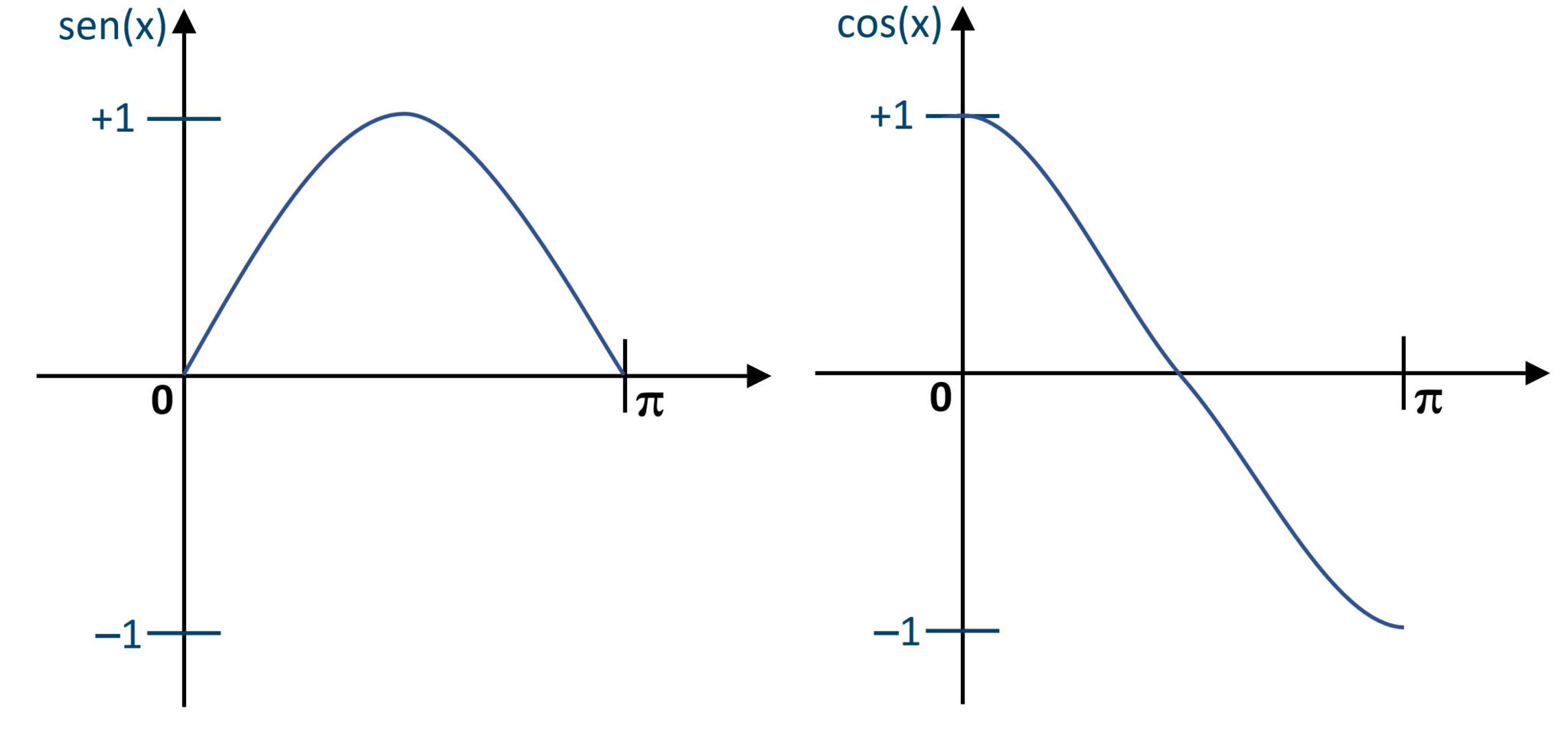
Osserviamo prima di tutto che la disequazione è strettamente positiva, con il segno di maggiore e non quello di maggiore o uguale. Questo comporta che se l'espressione assume il valore zero per qualche valore di x, allora per tali valori non è soddisfatta.
Studiamo "a pezzi" la funzione proposta dal quiz.
Il primo termine è cos(x)/2 che nell'intervallo [0, π) assume i valori:
–1/2 < cos(x)/2 ≤ +1/2
Ce consideriamo il termine cos(x)/2 + 1/2, questo assume i valori:0 < cos(x)/2 +1/2 ≤ +1
Il secondo termine è 2·sen(x) che nell'intervallo [0, π) assume i valori:
0 ≤ 2·sen(x) ≤ 2
Sommando le due parti cos(x)/2 +1/2 e 2·sen(x) che abbiamo valutato separatamente, possiamo affermare così che sicuramente l'espressione assume valori positivi; ci rimane da valutare se assume anche il valore zero, valore che sarebbe escluso dalla disequazione. Questo potrebbe accadere in uno dei due estremi 0 e π dell'intervallo di definizione della disequazione. l'estremo destro di valore π è stato pero escluso definendo l'intervallo come [0, π). Valutiamo solo l'estremo sinistro con x=0.
cos(0)/2 + 2·sen(0) + 1/2 = +1/2 + 0 +1/2 = 1
valore compatibile con la disequazione
Possiamo così affermare che la soluzione del quiz è la E) che riporta:
«La disequazione è verificata per ogni x appartenente all’intervallo assegnato»
OSSERVAZIONE SULLA VERSIONE UFFICIALE ERRATA DEL QUIZ
Il quiz è stato proposto ai candidati assegnando per i valori di x l'intervallo [0, π] che comprendeva anche l'estremo destro per x=π.
In tale versione bisognava valutare anche il valore x=π e risultava:cos(π)/2 + 2·sen(π) + 1/2 = –1/2 + 0 +1/2 = 0
valore INCOMPATIBILE con la disequazione
La soluzione in tal caso sarebbe dovuta essere tale da ridurre l'intervallo di definizione del solo estremo destro π .
E) 0 ≤ x < π
soluzione che mancava.
NESSUNA RISPOSTA VALIDA
Commento test medicina e odontoiatria 2021 |
|||
|---|---|---|---|
Rag.logico e Cult.generale | |||
Biologia | |||
Chimica | |||
Fisica e Matematica | |||


