Qual è l’insieme delle soluzioni reali della disequazione seguente?
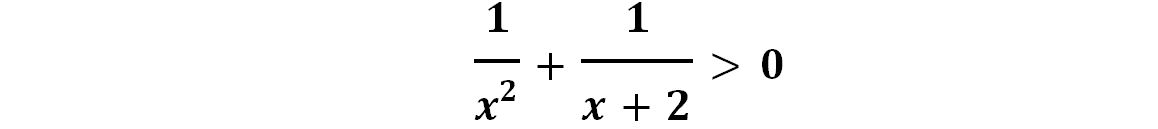
Seguiamo il procedimento canonico per lo studio della disequazione.
Come primo passaggio sommiamo le due frazioni ed otteniamo:
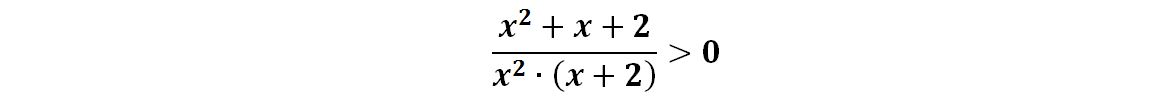
Come prima cosa individuiamo il campo di esistenza ponendo la condizione che il denominatore sia diverso da zero. Abbiamo:
C.E. : x≠0 e x≠-2
Ora studiamo la positività/negatività del numeratore e del denominatore (studio dei segni).
Al numeratore abbiamo x2+x+2 . Andando a risolvere l’espressione come equazione scopriamo che non ha soluzioni (infatti il discriminante ∆=b2-4ac=-7 risulta negativo) Perciò il numeratore sarà comunque sempre positivo.
Al denominatore abbiamo il prodotto di due termini: x2 che è sempre positivo e (x+2) che è l’unico fattore che può avere un valore positivo o negativo.
Perciò la positività/negatività dell’intera disequazione dipende da (x+2).
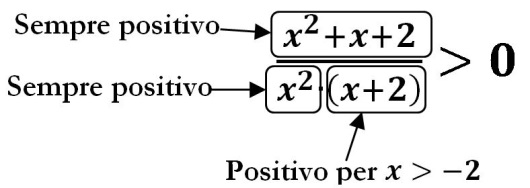
Tenendo conto del Campo di esistenza che ci fa scartare il valore x=0 avremo come soluzione:
x >-2 e x≠0


