Michele e Nicolò corrono ogni mattina partendo alle ore 06:00 dal solito incrocio. Michele corre lungo un percorso quadrato di lato di lato 200 m, Nicolò lungo un percorso quadrato di lato 400 m. I due, viaggiando costantemente alla stessa velocità di 2 m/s, percorrono assieme la prima parte per poi dividersi. Qual è il minimo intervallo di tempo dopo il quale i due potrebbero ritrovarsi per percorrere ancora un tratto insieme?
Per capire il quiz è necessario rappresentarlo con uno schema grafico.
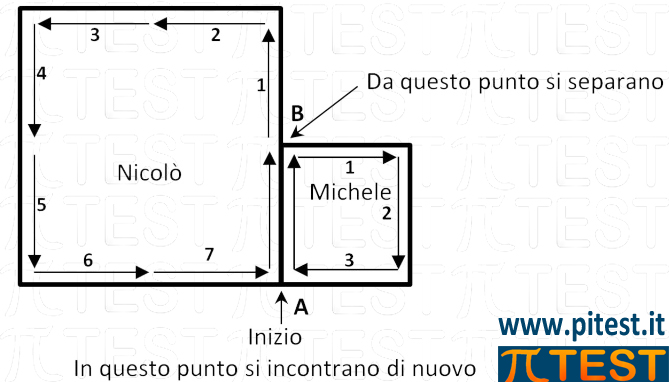
È utile individuare una certa lunghezza di percorso che sia associata ad un tempo. Consideriamo un lato del quadrato piccolo di 200 metri, che percorso alla velocità di 2 m/s richiede 100 secondi (t=sp/v=200/2=100s).
Le frecce riportate sul disegno equivalgono a 200 metri di percorso e a 100 secondi di tempo.
Nicolò per andare dal punto B (di separazione da Michele) al punto A (di incontro) impiega 700 secondi (7 frecce). Michele invece per andare da B ad A impiega solo 300 secondi (3 frecce); continua però a correre percorrendo per intero un altro quadrato aggiungendo altri 400 secondi ed impiegando complessivamente 700 secondi. I due amici così dopo 700 secondi si incontreranno.


