Quale/i dei seguenti sillogismi è/sono vero/i?
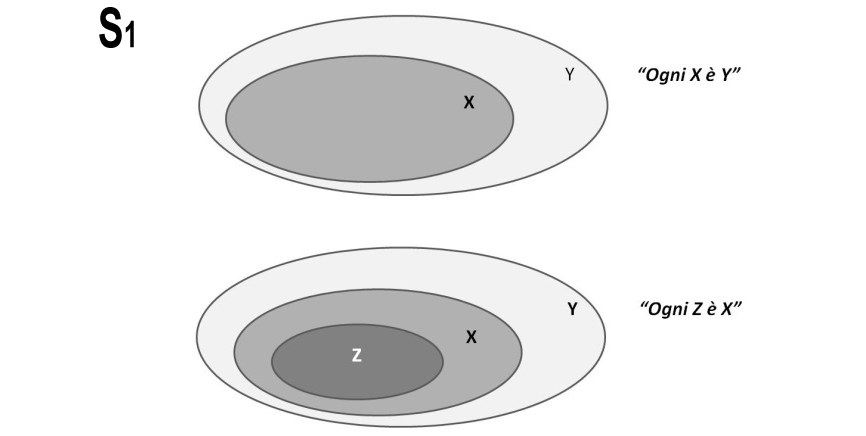
S1 ogni X è Y, ogni Z è X, allora ogni Z è Y
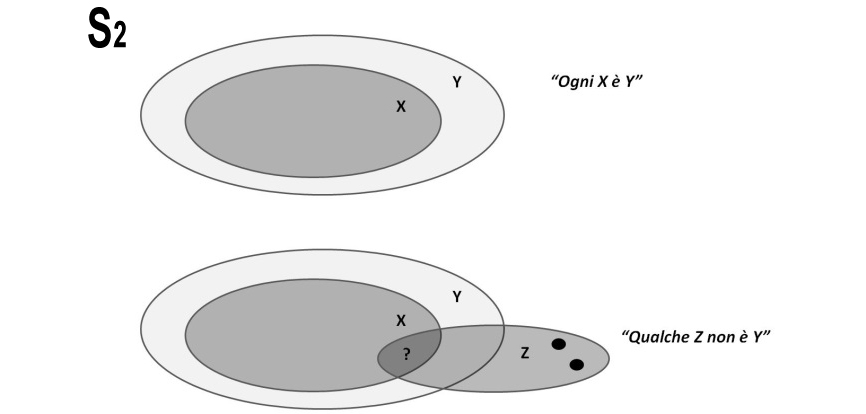
S2 ogni X è Y, qualche Z non è Y, allora qualche Z non è X
S3 nessun X è Y, qualche X è Z, allora qualche Z non è Y
Bisogna rappresentare i sillogismi attraverso l’insiemistica con i grafici di Eulero Venn ricordando che “tutti” significa che tra i due insiemi c’è un rapporto di inclusione, “qualche” significa che tra i due insieme esiste un’intersezione, “nessuno” significa che i due insiemi sono esterni e non condividono alcun elemento.
Dal grafico di Eulero Venn si deduce anche che ogni Z è Y. Il primo sillogismo è vero.
Dal grafico di Eulero Venn si deduce che Z non può essere incluso né in Y né in X.
Non si può dedurre nulla sull’eventuale intersezione tra Z e X, ricordiamoci che non possiamo dare per scontata né un’esclusione né un’intersezione tra questi due insiemi. Dal grafico di Eulero Venn si deduce anche che alcuni Z non sono X, se non altro quelli esterni anche a Y, rappresentati in figura da puntini. Il secondo sillogismo è vero.
Dal grafico di Eulero Venn si deduce che gli Z che appartengono anche a X, quelli rappresentati in figura da puntini, non possono appartenere a Y, quindi qualche Z non è Y. Il terzo sillogismo è vero.
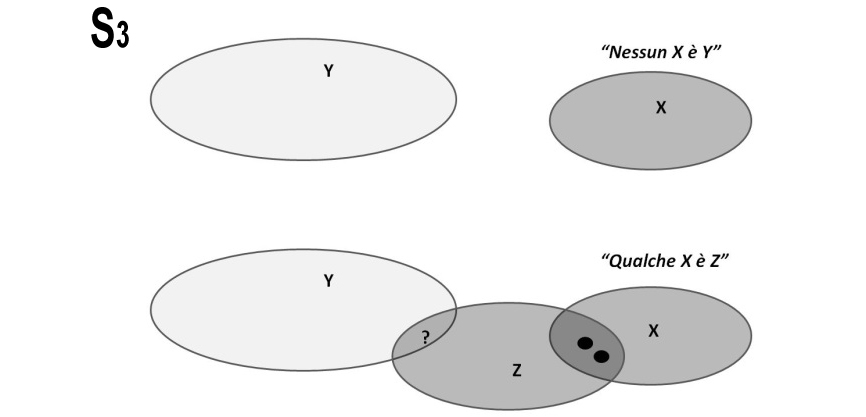
Come ulteriore osservazione, anche se non utile ai fini del quiz, diciamo che non si può dedurre nulla sull’eventuale intersezione tra Z e Y; non possiamo dare per scontata né un’esclusione né un’intersezione.


