Veterinaria 2010
In un ateneo, degli studenti iscritti, il 62% è di sesso maschile, il 36% è fuori corso ed il 9% è lavoratore.
Quale delle seguenti affermazioni è necessariamente vera?
Nell'ambito dei quiz "suddivisione in più categorie" questo è uno tra i quiz più complessi-lunghi da risolvere.
La totalità degli studenti iscritti, il 100%, è suddivisa in te diverse categorie: Maschi-femmine, fuori corso-in corso, lavoratori e non lavoratori secondo le percentuali date nel testo:

Valutiamo le affermazioni riportate nelle risposte. Il modo di procedere è quello di cercare di scartarle perché individuano situazioni non vere; allo stesso tempo, quando non è possibile scartarla, allora l'affermazione è vera e sarà la risposta che cerchiamo.
A) C'è almeno uno studente di sesso maschile fuori corso
Cerchiamo una distribuzione dei maschi e dei fuori corso che renda non vera l'affermazione A).
La risposta utilizza il quantificatore "almeno" che significa "al minimo" cioè almeno uno.
Nel grafico proviamo a sistemare i maschi in un estremo e i fuori corso nell'estremo opposto.

In questa distribuzione tutti i maschi non sono fuori corso. L'affermazione A) per essere vera lo deve essere in ogni caso. In questo caso non è vera e perciò non è sempre vera. Scartiamo l'affermazione A).
B) C'è almeno una studentessa lavoratrice
Procediamo come nel precedente caso.
La risposta utilizza il quantificatore "almeno" che significa "al minimo" cioè almeno una.
Cerchiamo una distribuzione delle femmine e dei lavoratori che renda non vera l'affermazione B).
Nel grafico proviamo a sistemare le femmine in un estremo e i lavoratori nell'estremo opposto.

In questa distribuzione tutti le femmine non sono lavoratrici. L'affermazione B) per essere vera lo deve essere in ogni caso. In questo caso non è vera e perciò non è sempre vera. Scartiamo l'affermazione B).
C) Non ci sono studenti lavoratori che non siano fuori corso
La risposta parla di studenti non specificando il sesso, specificazione che invece viene fatta nelle altre risposte. Si intende perciò parlare di studenti in generale a prescindere dal sesso.
Cerchiamo una situazione nella quale, contrariamente da quanto afferma la risposta C), ci siano studenti lavoratori che non siano fuori corso (non fuori corso = in corso).
Nel grafico proviamo a sistemare i lavoratori e in corso nello stesso estremo.

In questa distribuzione esistono studenti che allo stesso tempo sono lavoratori e non fuori corso.
L'affermazione C) per essere vera lo deve essere in ogni caso. In questo caso non è vera e perciò non è sempre vera. Scartiamo l'affermazione C).
D) C'è almeno una studentessa in corso e non lavoratrice
La risposta D) coinvolge tutte e tre le categorie: Maschi-femmine, fuori corso-in corso, lavoratori e non lavoratori.
La risposta utilizza il quantificatore "almeno" che significa "al minimo" cioè almeno una.
Andiamo a cercare la sovrapposizioni tra femmine e in corso. Si possono verificare vari tipi di sovrapposizione. Noi cerchiamo le situazioni massime e minime.

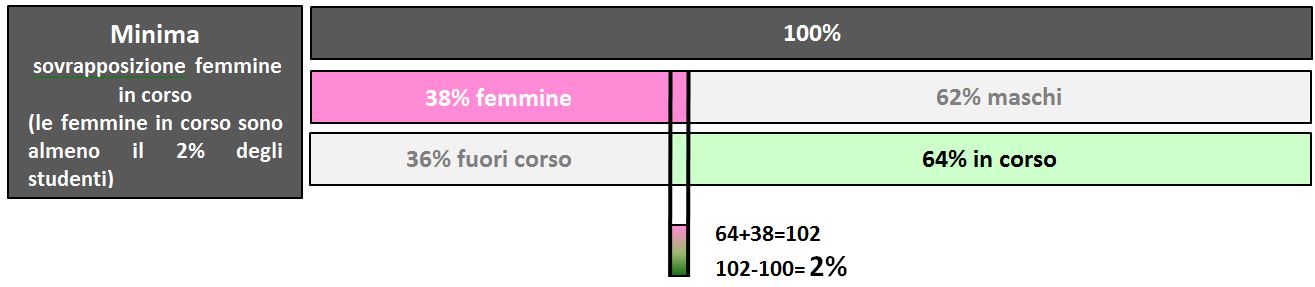
Per cercare di rendere falsa l'affermazione D) cerchiamo il minimo numero di femmine in corso. Sono, al minimo, 2.
Dobbiamo confrontare ora le 2 femmine in corso con i lavoratori, cercando la possibilità di non sovrapposizione (siamo alla ricerca della negazione della affermazione D).

In questa distribuzione tutti le femmine in corso non sono lavoratrici. L'affermazione D) per essere vera lo deve essere in ogni caso. In questo caso non è vera e perciò non è sempre vera. Scartiamo l'affermazione D).
Rimane ora l'ultima risposta E) che per esclusione deve essere quella corretta. Andiamo comunque a verificarla.
E) C'è almeno uno studente di sesso maschile che non è né lavoratore né fuori corso
Proviamo a negare questa affermazione dicendo il contrario, cioè che "NON c'è almeno uno studente di sesso maschile che non è né lavoratore né fuori corso". Se riusciamo a a dimostrare che è vera questa negazione della risposta E) potremmo scartarla, altrimenti la risposta sarà vera.
Realizziamo un grafico sovrapponendo al massimo i maschi con i fuori corso e con i lavoratori.
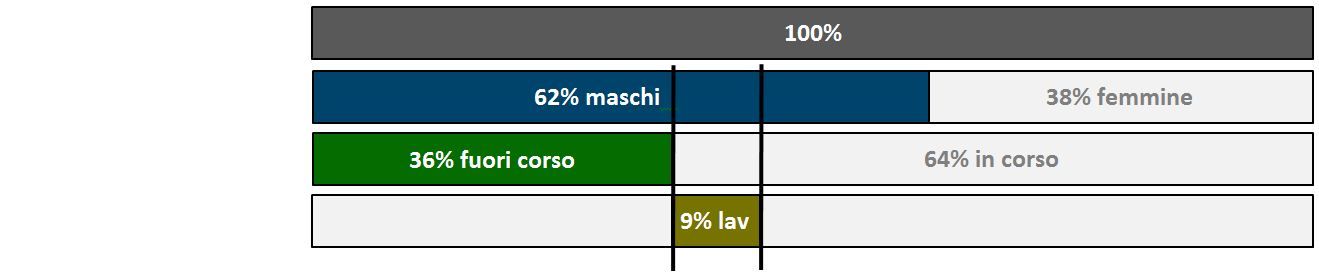
Nonostante la massima sovrapposizione che abbiamo realizzato rimane comunque qualche maschio che non è fuoricorso e non è lavoratore (per la precisione 62%–36%–9%=17%; il 17% degli studenti sono maschi non fuori corso e non lavoratori).
Concludiamo che, per quanto abbiamo cercato di escludere la presenza degli studenti di sesso maschile che non è né lavoratore né fuori corso, questi esistono sempre in ogni caso. Concludiamo che è CORRETTA l'affermazione D).
Osservazione finale. Abbiamo premesso all'inizio di questa spiegazione che questo quiz è complesso e lungo rispetto agli altri quiz simili di questo tipo (Suddivisione in più categorie). La difficoltà sta nel fatto che per ogni risposta bisogna impostare un confronto tra le categorie. Quiz simili più rapidi da risolvere impostano nella domanda un unico tipo di confronto come ad esempio il QUIZ 1.


