Per riuscire ad immaginare la situazione fissiamo un valore arbitrario del totale dei gettoni pari a 100.

“La metà di essi è quadrata e l'altra metà è rotonda” significa che 50 sono quadrati e 50 sono rotondi.

“I gettoni per metà sono verdi e per metà sono blu” significa che 50 sono verdi e 50 sono blu.

È immediato vedere che la risposta D) è corretta:

D) il numero di gettoni rotondi verdi è uguale al numero di gettoni quadrati blu

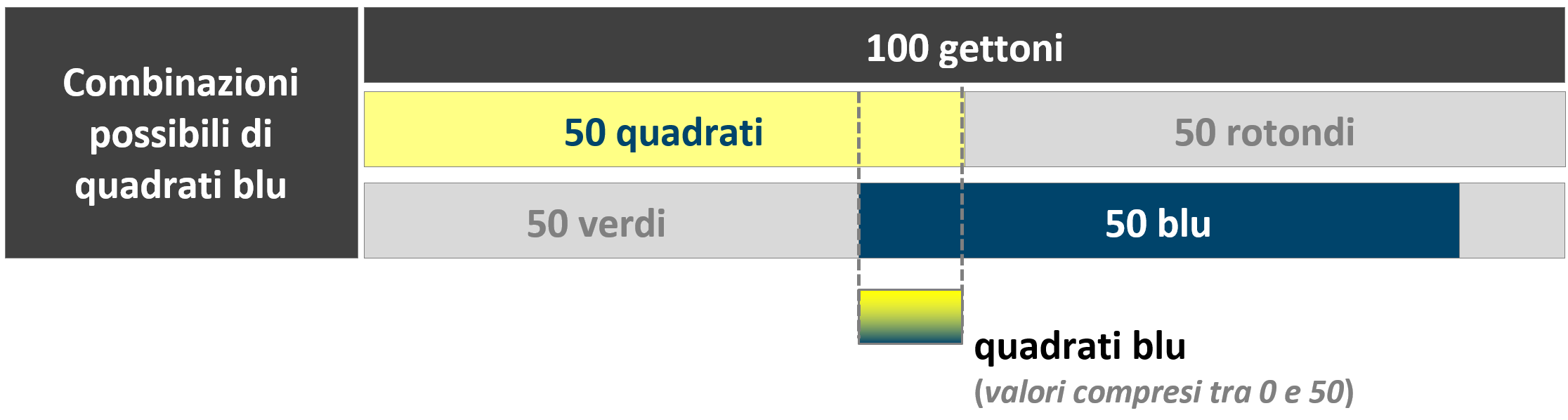
Le altre risposte A), B), C) ed E) prendono in considerazione le possibili combinazioni di gettoni con una forma e un colore (ad esempio gettoni quadrati blu). Le combinazioni possibili sono quattro: quadrati blu, quadrati verdi, rotondi blu e rotondi verdi. Il numero di gettoni presenti per ciascuna combinazione non è determinato ed oscilla da un minimo di zero ad un massimo di 50.

Vediamo ad esempio i gettoni quadrati blu.

Valutiamo le combinazioni estreme con il massimo ed il minimo possibile di gettoni quadrati blu:

Rappresentiamo anche le situazioni intermedie:

A questo punto è facile capire che le risposte A), B), C) ed E) fanno tutte affermazioni che risultano non sempre vere.