"Se qualcuno rimprovera Mauro, egli si offende. Ma se nessuno rimprovera Mauro, Ubaldo si arrabbia. Ieri Mauro non si è offeso". Se le precedenti affermazioni sono vere, è possibile dedurre che ieri:
1) Individuiamo tutte le regole presenti ed utilizziamo una lettera diversa per ciascuna proposizione
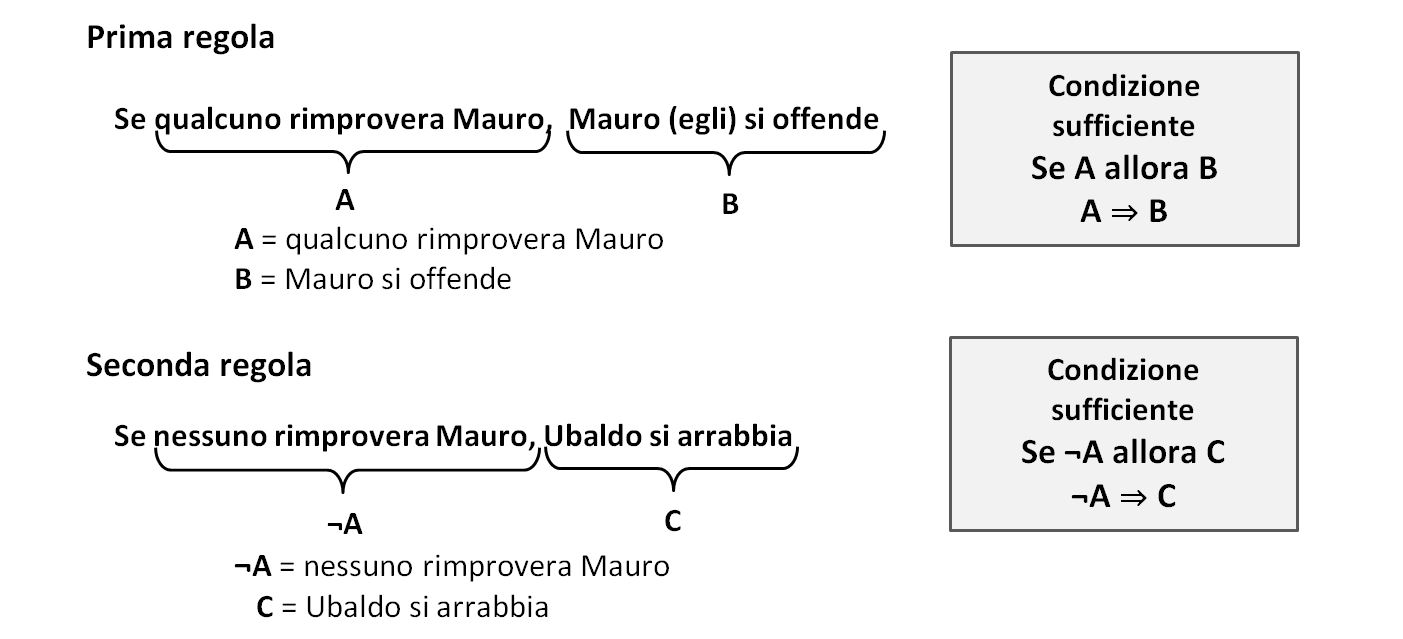
2) Mettiamo in grafico lo schema delle regole
A ⇒ B
¬A ⇒C
3) Per ciascuna delle due regole valutiamo il modus tollens. Questa fase è molto utile perché ci permette di avere un quadro completo di tutte le possibili alternative di implicazione.
Prima regola A → B
Per il modus tollens abbiamo ¬B ➔ ¬A
Seconda regola ¬A → C
Per il modus tollens abbiamo ¬C➔¬¬A ovvero (eliminando la doppia negazione) ¬C ➔ A
Riscriviamo le due regole con a fianco le varianti date dai rispettivi modus tollens:
| A ⇒ B | ¬B ⇒ ¬A |
| ¬A ⇒ C | ¬C ⇒ A |
Bisogna sempre fare questo schema prima di leggere le risposte del quiz per avere uno strumento veloce di analisi.
4) Analizziamo ora il CASO “Ieri Mauro non si è offeso”, ovvero ¬B.
¬B ci permette di dedurre ¬A. Prima deduzione
da ¬A possiamo poi dedurre C. Seconda deduzione
Complessivamente: ¬B ⇒ ¬A ⇒ C
Alla fine di questa analisi abbiamo individuato le seguenti situazioni:
¬B Ieri Mauro non si è offeso
¬A nessuno rimprovera Mauro
C Ubaldo si arrabbia
5) Analisi delle risposte.
A) Mauro non è stato rimproverato e Ubaldo non si è arrabbiato.
Ovvero ¬A e ¬C che non rispetta le deduzioni che abbiamo individuato.
B) Mauro è stato rimproverato e Ubaldo si è arrabbiato
Ovvero A e C che non rispetta le deduzioni che abbiamo già visto.
C) Ubaldo si è arrabbiato
Ovvero C che rispetta le deduzioni che abbiamo individuato. Risposta CORRETTA
D) Mauro è stato rimproverato e Ubaldo non si è arrabbiato
Ovvero A e ¬C che non rispetta le deduzioni che abbiamo individuato.
E) Mauro non si è offeso, ma potrebbe essere comunque stato rimproverato.
Ovvero ¬B e A che non rispetta le deduzioni che abbiamo individuato.


