Andrea possiede un mazzo di carte: su ogni carta sono segnati due numeri, uno su ogni faccia.
Nel suo mazzo, dietro ogni numero pari c’è un multiplo di 3. Ne consegue che, nel mazzo di carte di Andrea:
Per capire bene la regola “dietro ogni numero pari c’è un multiplo di 3”.
Immaginiamo alcune situazioni che la rispettano:
|
Possiamo avere una carta con il numero 2 (pari) e sul retro può esserci 3, oppure 6, oppure 9, ecc. |
|||
|
Possiamo avere una carta con il numero 4 (pari) e sul retro può esserci 3, oppure 6, oppure 9, ecc. |
|||
|
Possiamo avere una carta con il numero 1 (dispari) e sul retro può esserci qualsiasi numero dispari.
|
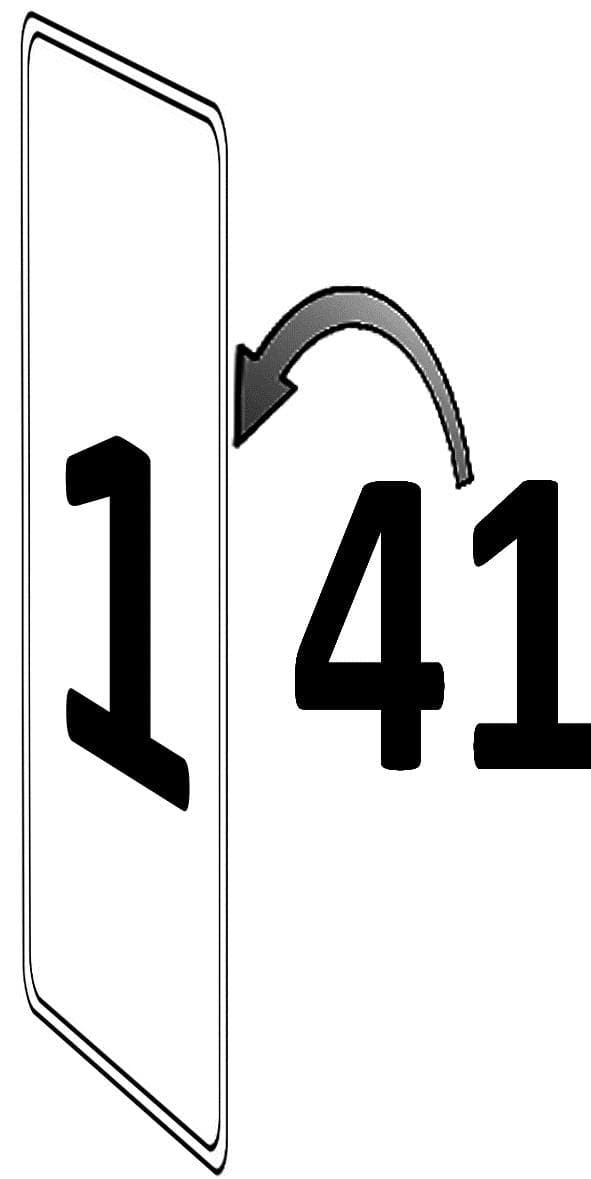 |
(7 e 41 sono numeri dispari presi come generico esempio) |
|
|
Possiamo avere una carta con il numero 3 (dispari) e sul retro può esserci qualsiasi numero dispari; oppure dietro può esserci anche un numero pari (un numero pari comporta un multiplo di tre sull’altra faccia) |
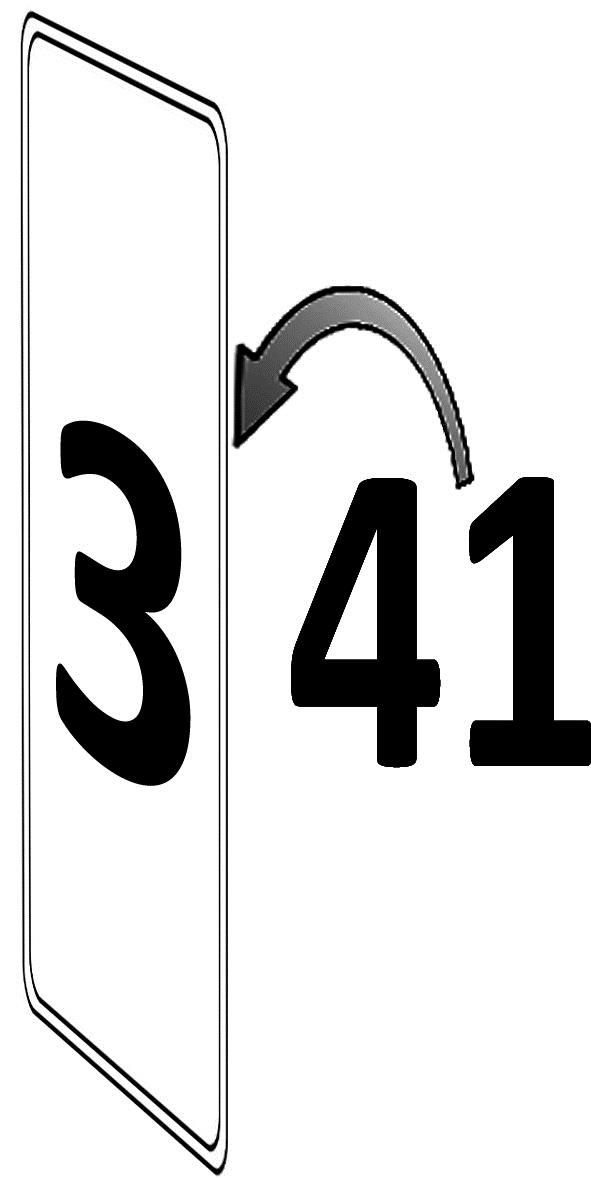 |
Verifichiamo le risposte per cercare quale esprime un’affermazione corretta:
A) nessuna carta può avere su un lato un numero doppio di quello che c’è sul lato opposto
Falso. Infatti ad esempio possiamo avere la carta con i numeri 6 e 12
B) se su un lato c’è 15, sull’altro lato non ci può essere 7
Falso. Sul retro di un numero dispari può esserci qualsiasi numero
C) nessuna carta può avere lo stesso numero su entrambi i lati
Falso. Sul retro di un numero dispari può esserci qualsiasi numero e ad esempio possiamo avere la carta con i numeri 1 e 1 e tra i pari possiamo avere 6, 6 o 12, 12.
D) una carta può contenere 3 su un lato e 5 sull’altro
VERO. Sul retro di un numero dispari può esserci qualsiasi numero
E) ci può essere una carta che contiene 11 su un lato e 18 sull’altro
Falso. Sul retro del numero 18 deve esserci un multiplo di 3.
La risposta corretta è la D)


