Alla nonna hanno rubato la crostata e lei sa che deve essere stato almeno uno dei suoi nipotini, Pim, Pom e Pam. Sa che se Pim è colpevole e Pom è innocente, allora Pam è colpevole. Che cosa si può dedurre?
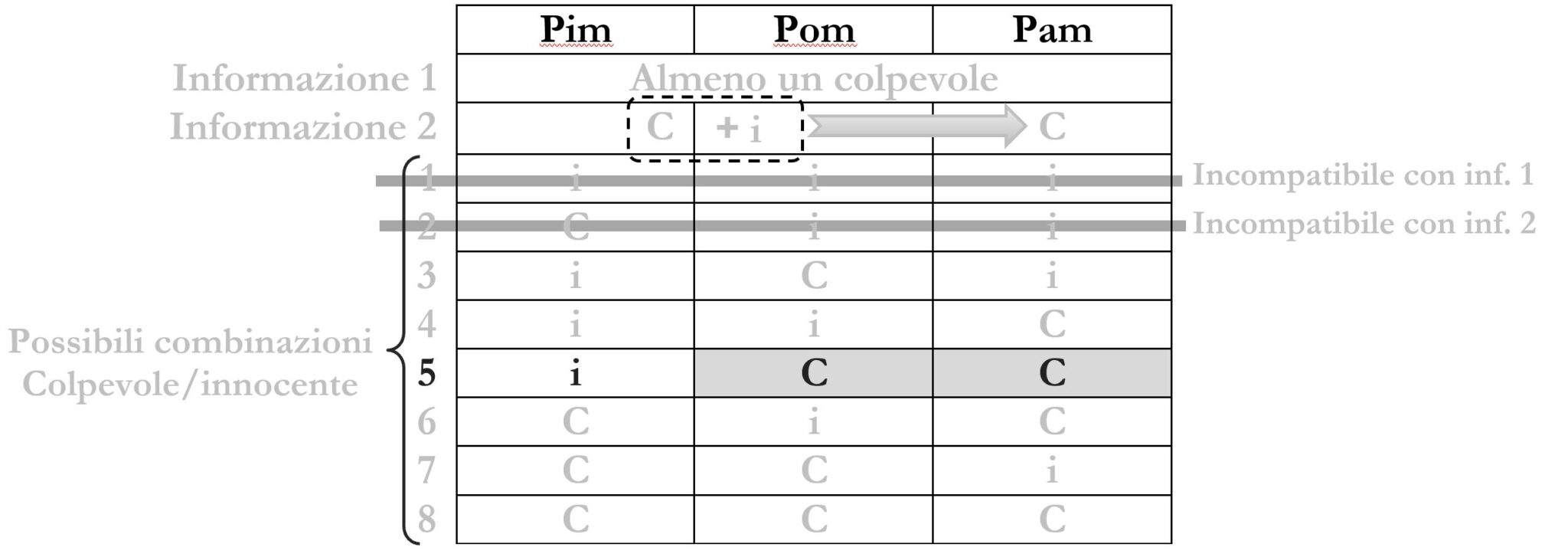
Impostiamo una tabella con tre colonne per i tre nipotini Pim, Pom e Pam nella quale scrivere le informazioni.
Abbiamo due informazioni (che assumiamo come Regole da considerare sempre vere):
Informazione 1: deve essere stato almeno uno dei suoi nipotini
Informazione 2: se Pim è colpevole e Pom è innocente, allora Pam è colpevole
Scriviamo le informazioni sul grafico.
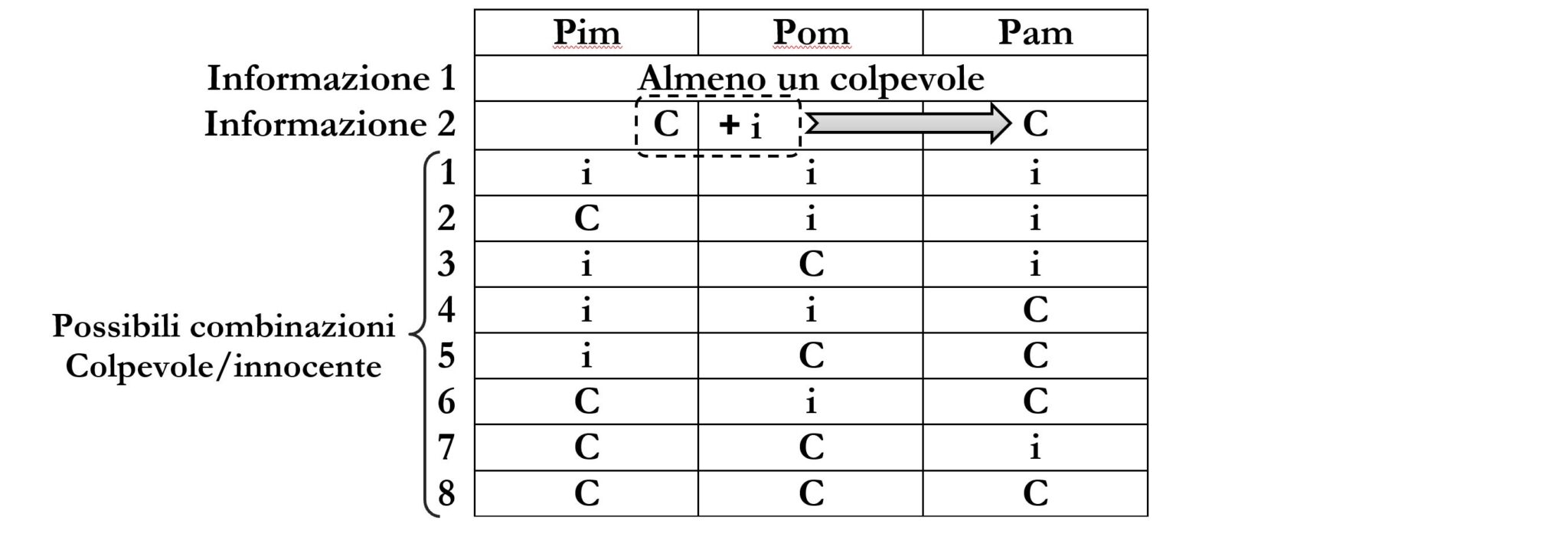
Sviluppiamo tutte le possibili combinazioni come nella seguente tabella.
COME CREARE UNA TABELLA CON TUTTE LE POSSIBILI COMBINAZIONI SENZA SALTARNE NESSUNANello sviluppo di tutte le combinazioni bisogna evitare di tralasciarne alcune. Si suggerisce il seguente metodo per sviluppare tutte le possibili combinazioni Colpevole/Innocente. Si sviluppano tutte le combinazioni possibili ponendo, in ordine: nessun colpevole / un colpevole / due colpevoli / tre colpevoli a) nessun colpevole 
b) un colpevole Consideriamo un colpevole e due innocenti; piazziamo il colpevole “C” nella prima, poi nella seconda ed infine nella terza colonna e posizioniamo la “i” di innocente nelle rimanenti celle.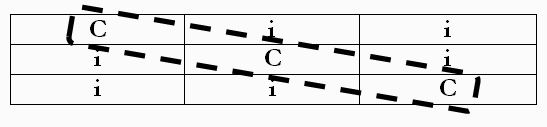 
c) due colpevoli Poi consideriamo due colpevoli e un innocente; piazziamo l’innocente “i” nella prima, poi nella seconda ed infine nella terza colonna e posizioniamo la “C” di colpevole nelle rimanenti celle.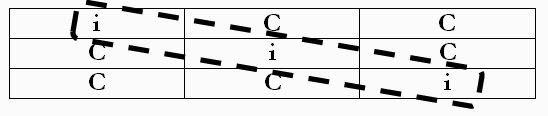 
c) tre colpevoli Infine consideriamo tre “C ” |
Adesso andiamo a valutare quali situazioni sono incompatibili con le regole e quali invece sono possibili.
La combinazione 1 è incompatibile con l’informazione 1. La combinazione 2 è incompatibile con l’informazione 2.
Le combinazioni rimaste sono tutte possibili.
La situazione rimane indefinita perché il quiz non ci dà sufficienti informazioni per individuare con esattezza colpevoli ed innocenti. Passiamo così a valutare le risposte per andare ad individuare una affermazione che risulti assolutamente certa.
La risposta A) afferma che c’è almeno un colpevole fra Pim e Pom. Se è vera deve esserlo sempre. Analizziamo se risulta in ogni possibile combinazione.
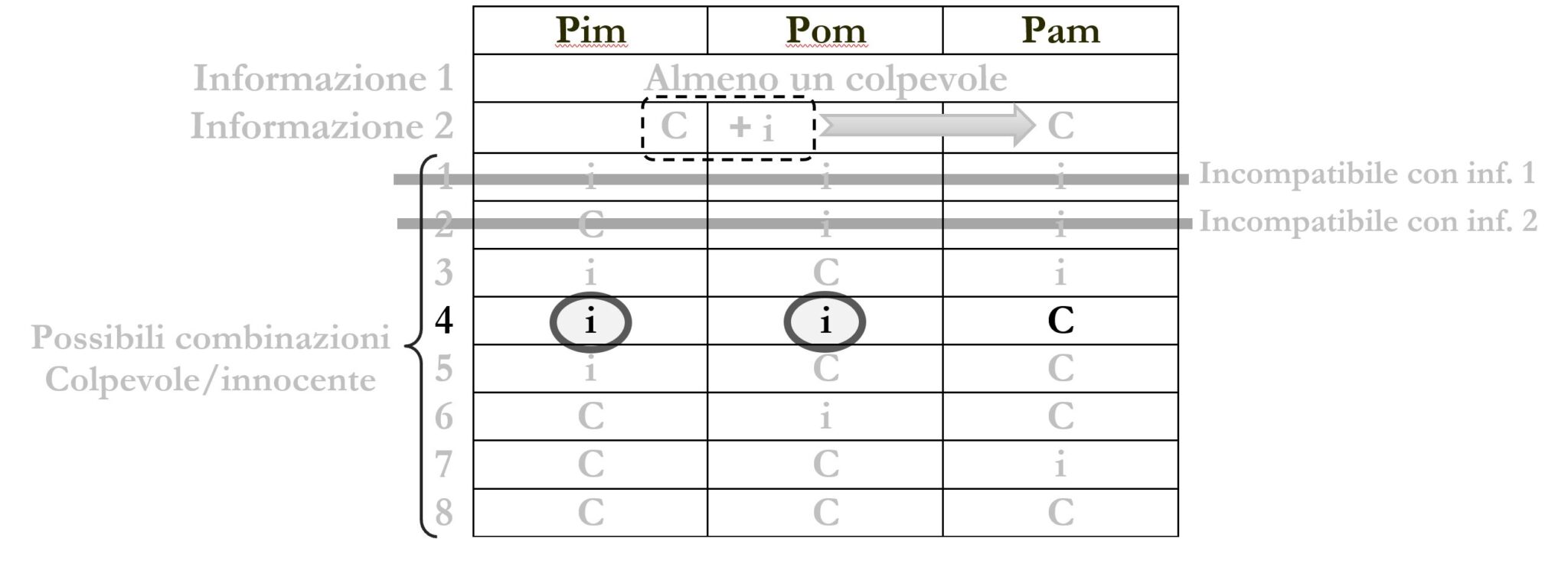Nella combinazione 4 non c’è un colpevole tra Pim e Pom. Perciò non possiamo affermare che è sempre sicuramente vero che “c’è almeno un colpevole fra Pim e Pom”. Escludiamo perciò anche la risposta A).
La risposta B) afferma che c’è almeno un colpevole fra Pim e Pam. Se è vera deve esserlo sempre. Analizziamo se risulta in ogni possibile combinazione.
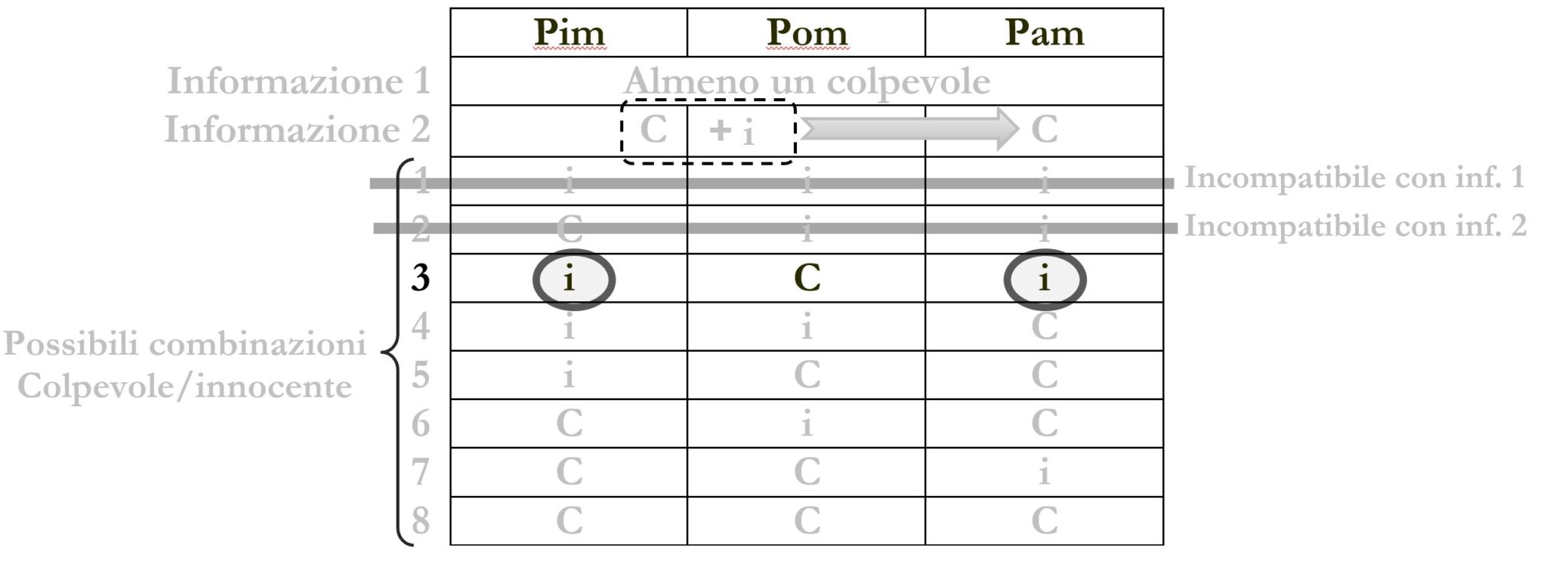
Nella combinazione 3 non c’è un colpevole tra Pim e Pam. Perciò non possiamo affermare che è sempre sicuramente vero che “c’è almeno un colpevole fra Pim e Pam”. Escludiamo perciò anche la risposta B).
La risposta C) afferma che i colpevoli sono almeno due. Se è vera deve esserlo sempre Analizziamo se risulta in ogni possibile combinazione.
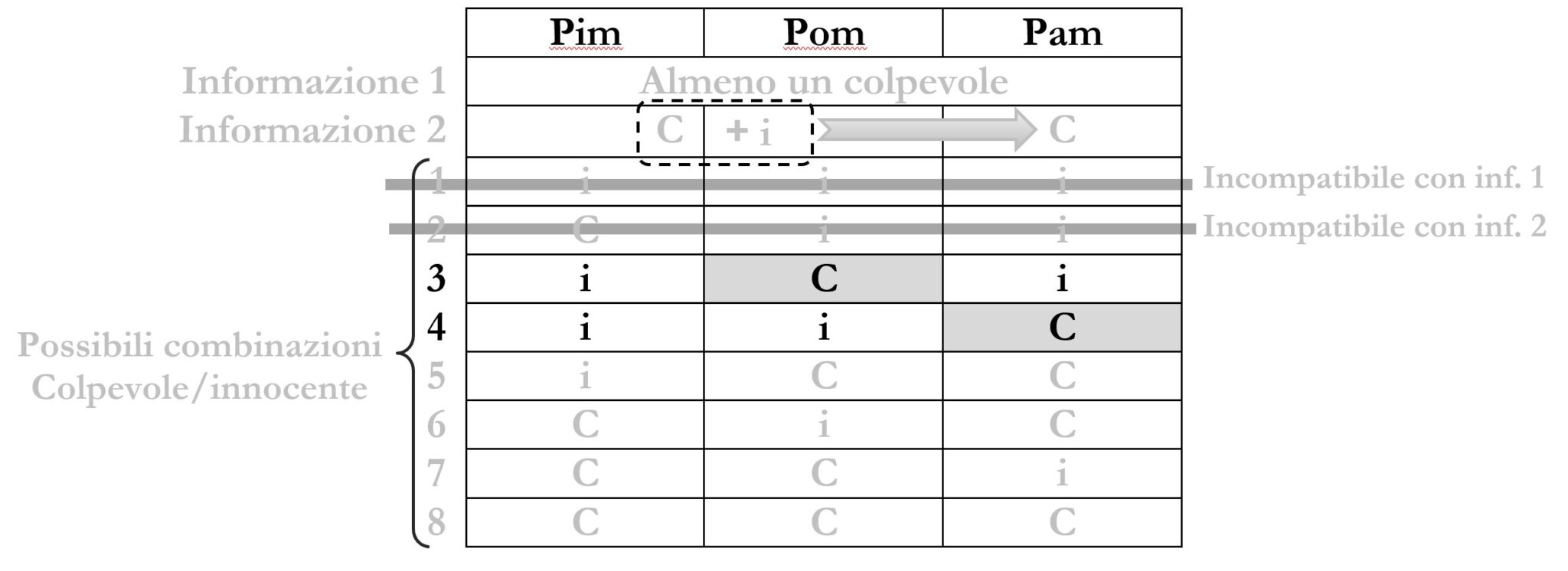Nelle combinazioni 3 e 4 c’è un solo colpevole. Perciò non possiamo affermare che è sempre sicuramente vero che “i colpevoli sono almeno due”. Escludiamo perciò anche la risposta C).
La risposta D) afferma che c’è almeno un colpevole fra Pom e Pam. Se è vera deve esserlo sempre. Analizziamo se risulta sempre così.
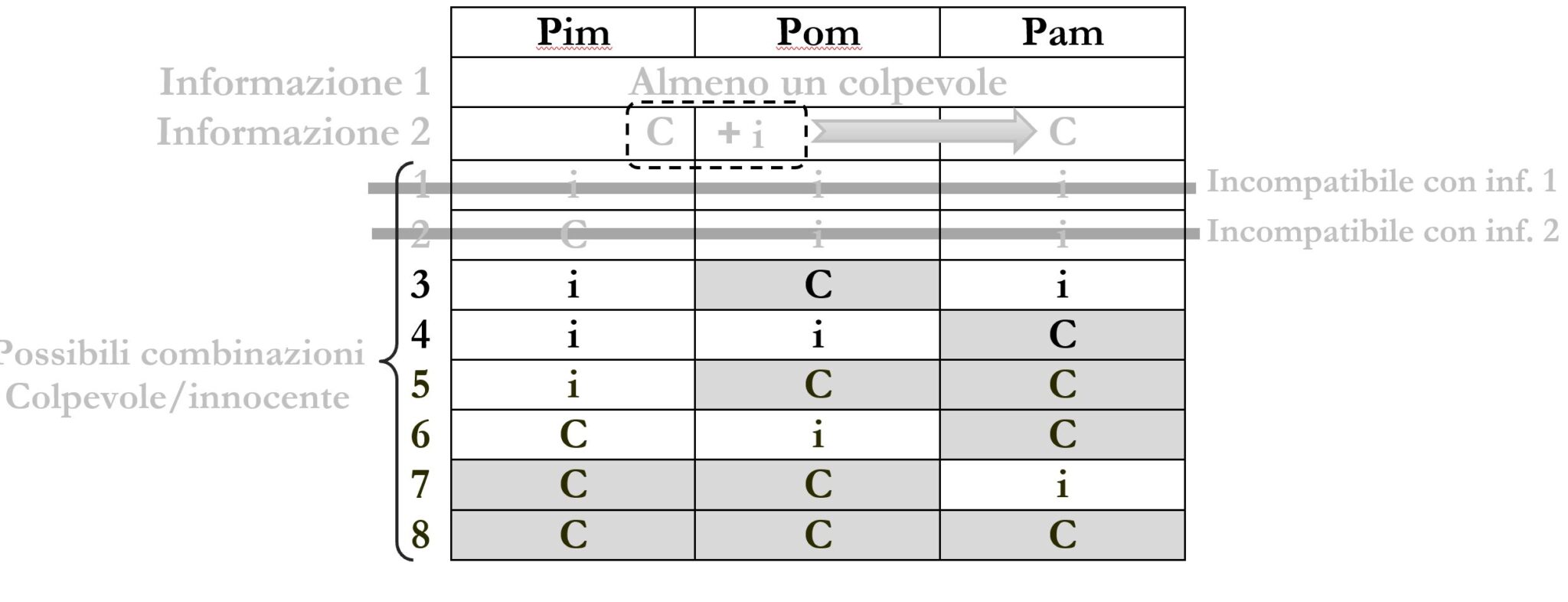In tutte le combinazioni c’è sempre almeno un colpevole tra Pom e pam.
La risposta corretta è la D)
La risposta E) è errata perché nella combinazione 5 abbiamo due colpevoli.
