Incontro due persone nel paese dei cavalieri (che dicono sempre la verità) e dei furfanti (che mentono sempre).
Il primo dice: Siamo entrambi ricchi
Il secondo afferma: Siamo entrambi furfanti
Dunque necessariamente:
Prepariamo una tabella a due colonne sulla quale andremo a scrivere le regole del problema. Due colonne sono per le due persone coinvolte nel quiz e una per indicare chi sta parlando. Sulle righe scriveremo cosa viene detto delle figure coinvolte.

La prima informazione è costituita dalla affermazione del primo che dice: “Siamo entrambi ricchi”.
Riportiamo l’affermazione così come è stata pronunciata. Ci riserviamo di verificare se è vera o falsa in base a quanto emergerà in seguito.

La seconda affermazione “Siamo entrambi furfanti ” è difficile da gestire. Impariamo a riconoscerla perché quando si incontra in un quiz bisogna saperla utilizzare senza doversi mettere a fare lunghe riflessioni.
Nel ragionamento qui di seguito evidenziato analizziamo un tipo particolare di affermazioni che riguardano l’essere bugiardi. Applicheremo poi al presente quiz le conclusioni che abbiamo esaminato.
AUTO-AFFERMAZIONI CONCERNENTI L’ESSERE BUGIARDIPer affrontare l’affermazione “Siamo entrambi furfanti ” consideriamo prima un caso particolare studiato dalla linguistica e dalla filosofia: il paradosso del mentitore. Il paradosso del mentitore considera l’affermazione “io sono bugiardo”. Un’affermazione che nessuno riuscirà mai a dimostrare se è falsa o vera. L’affermazione paradossale del mentitore riguarda una persona che parla di se stesso. La situazione cambia però nel momento che una persona fa una affermazione su se stessa unitamente ad un’altra persona dicendo “siamo entrambi bugiardi”. Sviluppiamo tutte le combinazioni possibili tra le due persone che possono essere bugiarde o veritiere e per ogni combinazioni verifichiamo se è congruente o se si creano contraddizioni. 
Nel caso 1, colui che fa la affermazione è posto come veritiero e la sua affermazione “siamo entrambi bugiardi” dovrebbe di conseguenza essere vera, in contraddizione col senso della frase. La combinazione 1 è perciò da scartare per contraddizione. Anche nel caso 2, colui che fa la affermazione è veritiero e per lo stesso ragionamento del caso 1 scartiamo la combinazione. Nel caso 3, colui che fa la affermazione è bugiardo e deve mentire. Invece di mentire sta affermando la verità, cioè che sono entrambi bugiardi. Questa affermazione veritiera è in contraddizione con il suo stato di bugiardo. La combinazione 3 è perciò da scartare perché non è coerente. Nel caso 4 colui che fa la affermazione è bugiardo e la sua affermazione deve essere falsa. Infatti la sua affermazione è “Siamo entrambi bugiardi” risulta falsa perché l’altro è veritiero. Questo caso è l’unico che non porta a contraddizione. La combinazione chi afferma-bugiardo e altro-veritiero è l’unica congruente con l’affermazione. 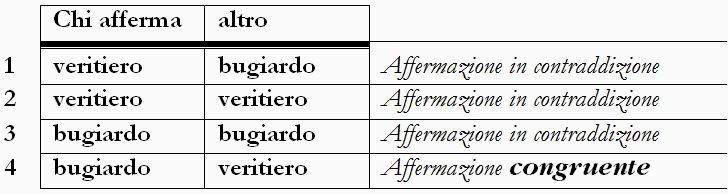
Solo il quarto caso presenta una situazione congruente. E di conseguenza dovremo assumere che è questa la combinazione accettabile. Se estendiamo questo ragionamento alla affermazione “siamo tutti bugiardi”, rivolta ad un gruppo di persone, possiamo dimostrare che equivale al fatto che chi parla è bugiardo e almeno una persona tra gli altri non è bugiarda. Una sintesi di questo ragionamento può essere la seguente: ♦ l’affermazione “io sono bugiardo” è un paradosso. ♦ l’affermazione “io e te siamo bugiardi ” comporta che: io sono bugiardo tu non sei bugiardo ♦ l'affermazione “siamo tutti bugiardi ” comporta che: io sono bugiardo almeno una persona tra gli altri non è bugiarda |
Ritorniamo al quiz. La affermazione della seconda persona “Siamo entrambi furfanti” comporta che il secondo è bugiardo (colui che afferma) e il primo è veritiero. Riportiamo questo nella tabella iniziale con i termini Cavaliere = veritiero e Furfante = bugiardo.

A questo punto l’affermazione del primo, che è veritiero, “Siamo entrambi ricchi” risulta vera.
Se andiamo ad analizzare le risposte vediamo che la risposta corretta è la C): il primo è un cavaliere, il secondo è ricco.
La risposta corretta è la C)


