Una bilancia a bracci in condizioni di equilibrio prevede l’uguaglianza delle masse presenti sui due piatti. È un modo grafico per proporre uguaglianze.

Abbiano Cubi, Sfere e Piramidi il cui numero chiamiamo C, S e P.

Le uguaglianze proposte sono:

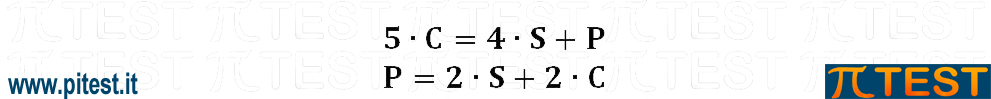Il quiz chiede di esprimere P in funzione di C.

Cerchiamo passaggi algebrici agevoli e veloci.

La seconda espressione esprime P in funzione di C e di S. Prevediamo di utilizzarla per esprimere P in funzione solamente di C come richiede la domanda. Ci serve una espressione che ci permetta di esprimere S in funzione di C.

La presenza della prima relazione sicuramente ci permetterà di ricavare quello che cerchiamo. Sostituiamo P nella prima espressione ed otteniamo:

Dalla quale ricaviamo:

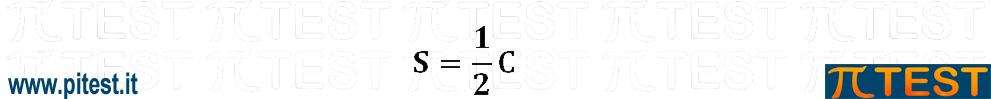
Questa espressione di S ci permette di giungere alla soluzione andando a sostituire:

---

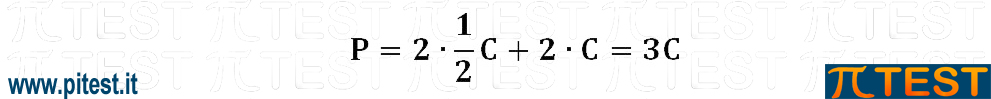
Procedimento alternativo

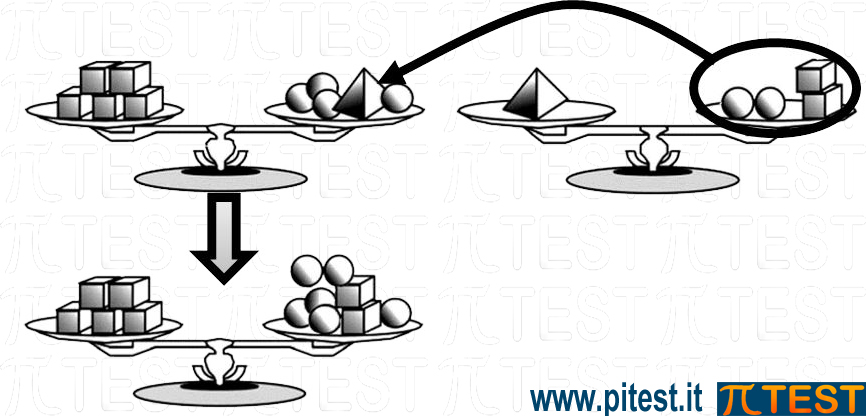
Possiamo anche seguire un ragionamento “grafico”. Sostituiamo nella prima bilancia la piramide con ciò che è contenuto nel secondo piatto della seconda bilancia, cioè due sfere e due cubi. Abbiamo ottenuto l’uguaglianza 5C=6S+2C
Eliminiamo due cubi a sinistra e a destra rispettando l’equilibrio della bilancia: Abbiamo ottenuto alla quale otteniamo 3C= 6S dalla quale, semplificando per 3, ricaviamo che due sfere equivalgono ad un cubo C = 2S .
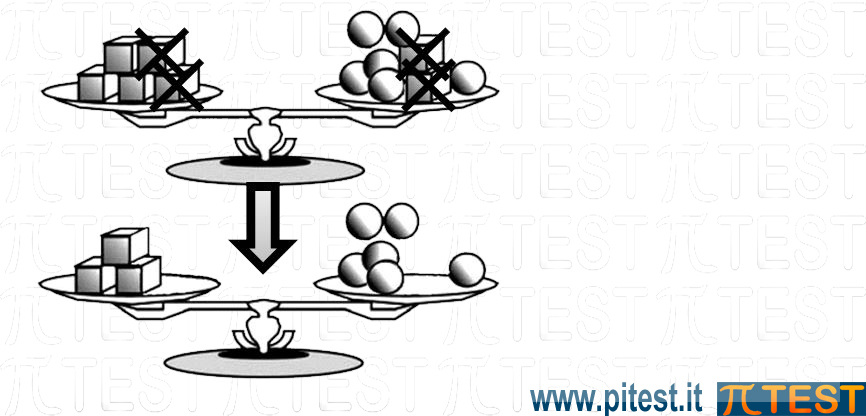Utilizziamo questa equivalenza appena detta: nella seconda bilancia sostituiamo le due sfere presenti con un cubo.

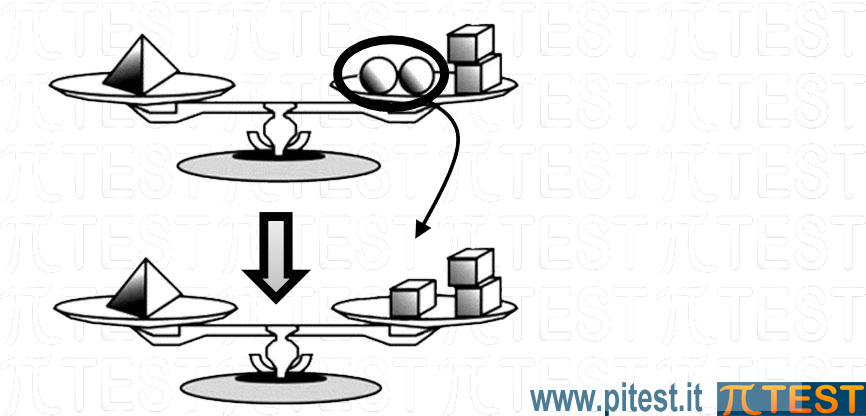Abbiamo così ottenuto la soluzione del quiz. Una piramide equivale a tre cubi.

Anche con questo metodo otteniamo la risposta D)