Quale/i dei seguenti sillogismi è/sono vero/i?
S1 nessun X è Y, qualche Y è Z, allora qualche Z non è X
S2 nessun X è Y, ogni Y è Z, allora ogni Z non è X
S3 ogni X è Y, qualche Z non è Y, allora qualche Z non è X
Bisogna rappresentare i sillogismi attraverso l’insiemistica ricordando che “tutti” significa che tra i due insiemi c’è un rapporto di inclusione, “qualche” significa che tra i due insieme esiste un’intersezione, “nessuno” significa che i due insiemi sono esterni e non condividono alcun elemento.
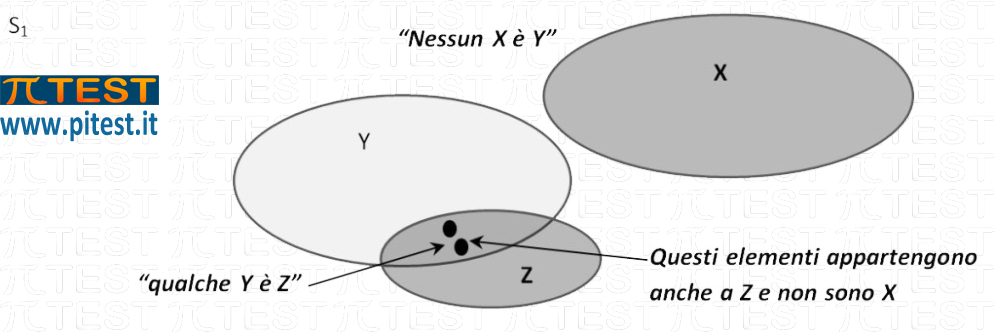
Dal grafico di Eulero Venn si deduce anche che qualche Z (quegli elementi di Y che sono anche Z) non è X. Il primo sillogismo è vero.
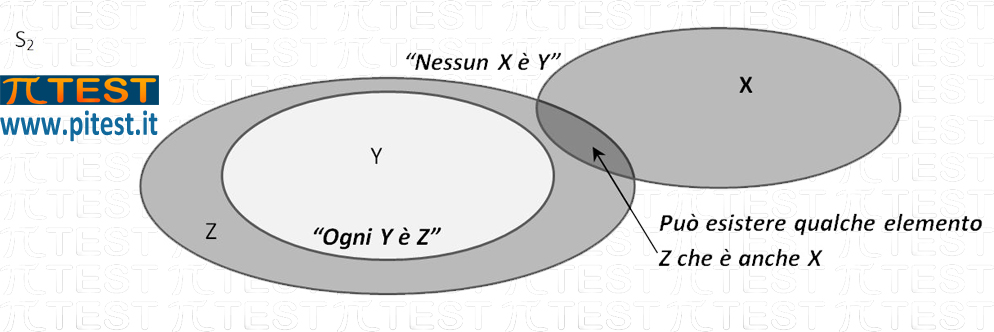
L’insieme Z, che include l’insieme Y, può essere abbastanza grande da contenere anche elementi di X (non necessariamente, ma solo come possibilità). Questo però toglie la verità al secondo sillogismo.
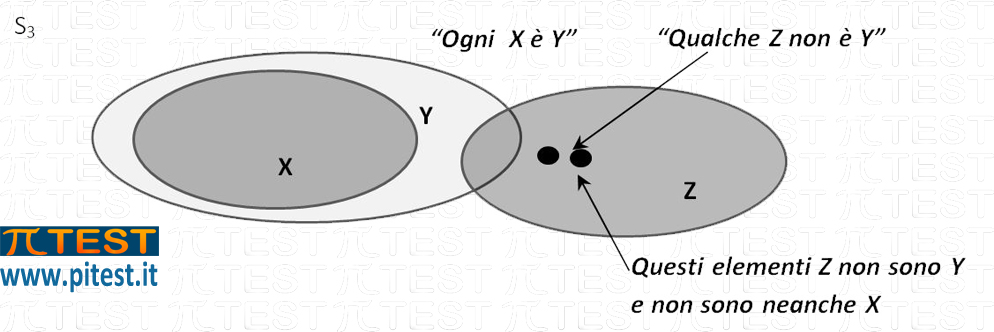
Dal grafico di Eulero Venn si deduce che gli Z che non sono Y, non sono neanche X. Il terzo sillogismo è vero.


