Ci lasciamo guidare dalle risposte che presentano i possibili valori

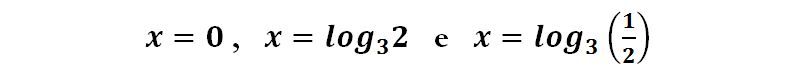
Per le proprietà degli esponenziali e dei logaritmi sappiamo che il logaritmo è la funzione inversa dell’esponenziale e che perciò quando applichiamo alla funzione la sua funzione inversa otteniamo il valore della variabile, ovvero:

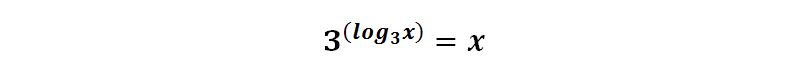
Ad esempio:

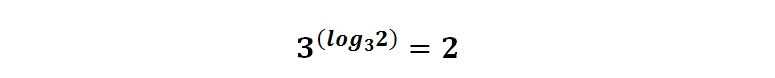
Cerchiamo opportuni passaggi che ci permettano di individuare “ 3^x “ all’interno dell’equazione.

9^x può essere visto come (3²)^x = 3^2x = (3^x)²

3^x+1 può essere visto come 3·3^x

Riscriviamo così l’equazione:

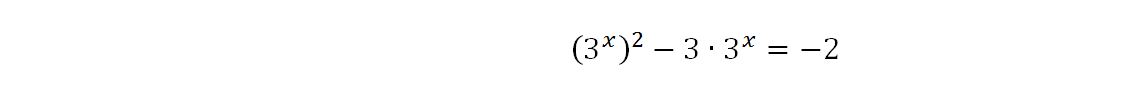
Verifichiamo i valori proposti nelle soluzioni:

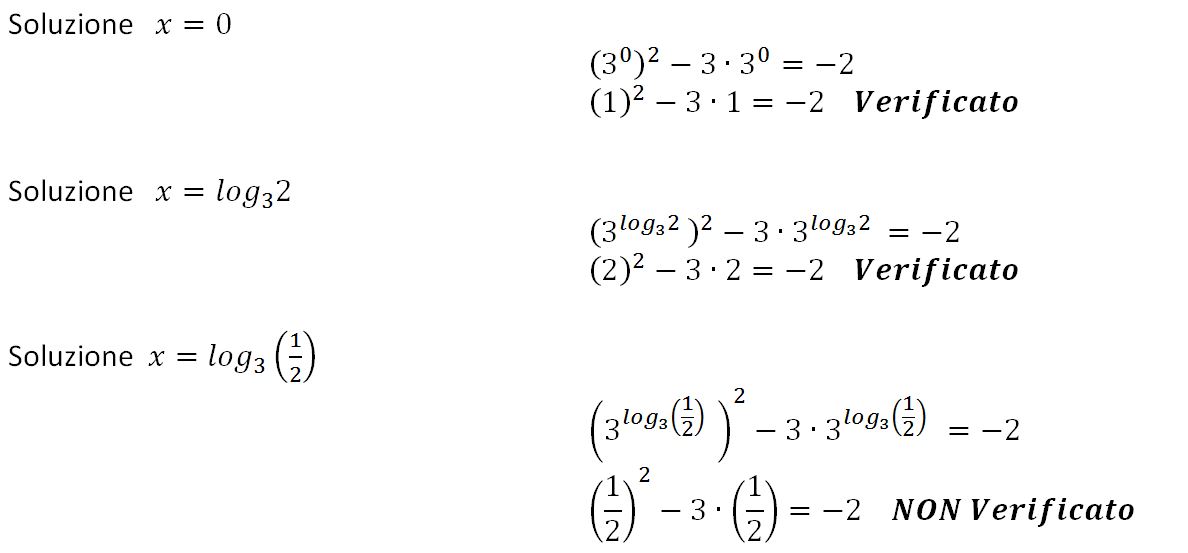
Metodo alternativo

Nell’equazione

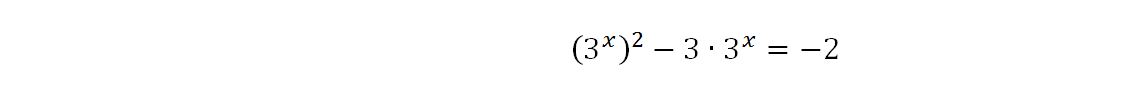
poniamo z= 3^x

Avremo l’equazione di secondo grado: z²-3·z = -2

Che ammette come soluzioni z=1 e z=2

Che riportano a:

3^x = 1 ⇒ x = 0

e

3^x = 2 ⇒ x = log₃ 2