Bisogna precisare subito che il testo sarebbe stato più chiaro se avesse aggiunto il termine “entrambi” formulando così l’affermazione iniziale: “Scegliendo a caso due allievi della classe prima, composta da 21 allievi, una volta su due gli studenti scelti portano entrambi gli occhiali.”.

Quando si parla di un numero imprecisato di persone e si afferma qualcosa riguardo il rapporto tra un certo sottogruppo ed il totale, siamo nel campo del calcolo della probabilità. In questo caso il sottogruppo è formato da due elementi che sono caratterizzati dal portare entrambi gli occhiali.

La probabilità che andiamo a cercare è una probabilità composta che si calcola dal prodotto delle probabilità dei due singoli fenomeni.

Chiamiamo x il numero di allievi che porta gli occhiali. Il primo fenomeno è definibile come un allievo all’interno degli x-1 porta gli occhiali; il secondo fenomeno è definibile come un allievo degli porta gli occhiali.

Il primo fenomeno ha una probabilità di accadere P₁=x/21.

Per il secondo fenomeno dobbiamo tener conto che dal gruppo iniziale abbiamo già preso un ragazzo con occhiali e che di conseguenza il numero di ragazzi con occhiali è ora x-1 su un totale di 21-1=20 ragazzi; la probabilità del secondo fenomeno perciò è P₂=(x-1)/21.

La probabilità composta sarà

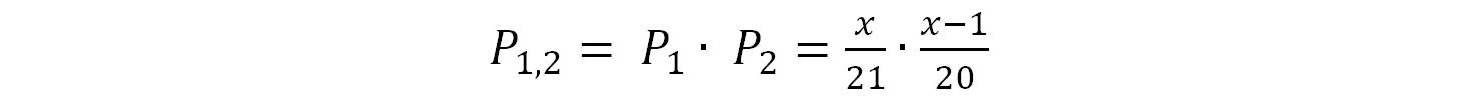
Il testo ci dice che tale probabilità composta P_1,2 ha una frequenza di una volta su due che corrisponde alla probabilità di 1/2.

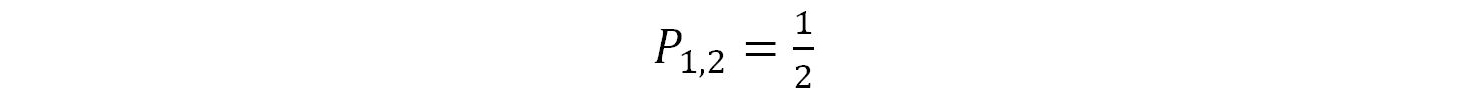
Possiamo così impostare la seguente equazione:

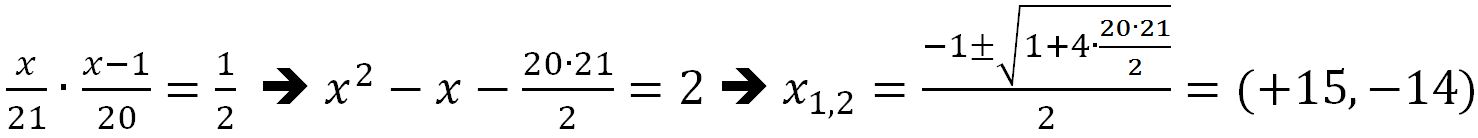
Consideriamo solo il risultato positivo +15 in quanto il valore -14 non ha significato fisico.

In alternativa alla soluzione di una equazione si può procedere verificando le risposte.

Risposta A), 9. Se gli studenti che portano gli occhiali sono 9, allora la probabilità che due studenti portino gli occhiali è (9/21)·(8/20)≠1/2

Risposta B), 11. Se gli studenti che portano gli occhiali sono 11, allora la probabilità che due studenti portino gli occhiali è (11/21)·(10/20)≠1/2

E così via fino alla risposta D), 15. avremo (15/21)·(14/20)=1/2