Le tavole di verità sono tabelle usate nella logica per determinare se, attribuiti i valori di verità alle proposizioni che la compongono, una determinata proposizione è vera o falsa. Le tavole di verità della congiunzione “e” (˄), dell’implicazione (⇒) e della negazione “non” (¬) sono rispettivamente:

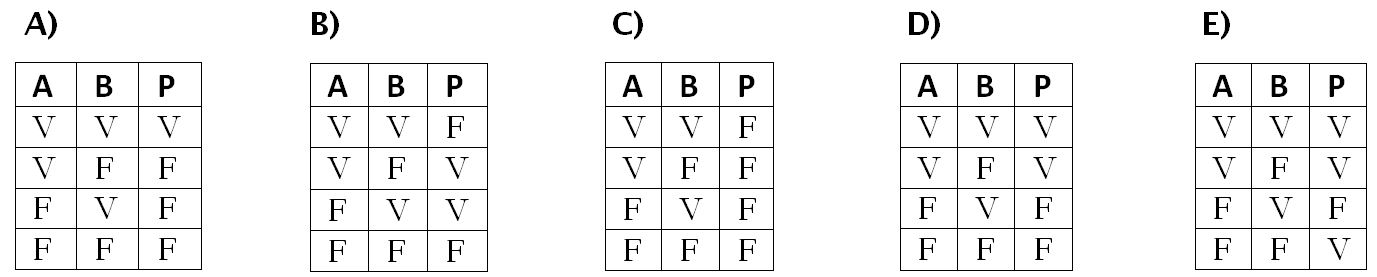
Qual è la tabella di verità della proposizione P: (¬A ⇒ B) ˄ A ?
Per costruire la tavola di verità dalla proposizione (¬A ⇒ B) ˄ A , INIZIAMO PER GRADI affiancando inizialmente alla tavola i valori di ¬A e B per poi operare l’implicazione ⇒
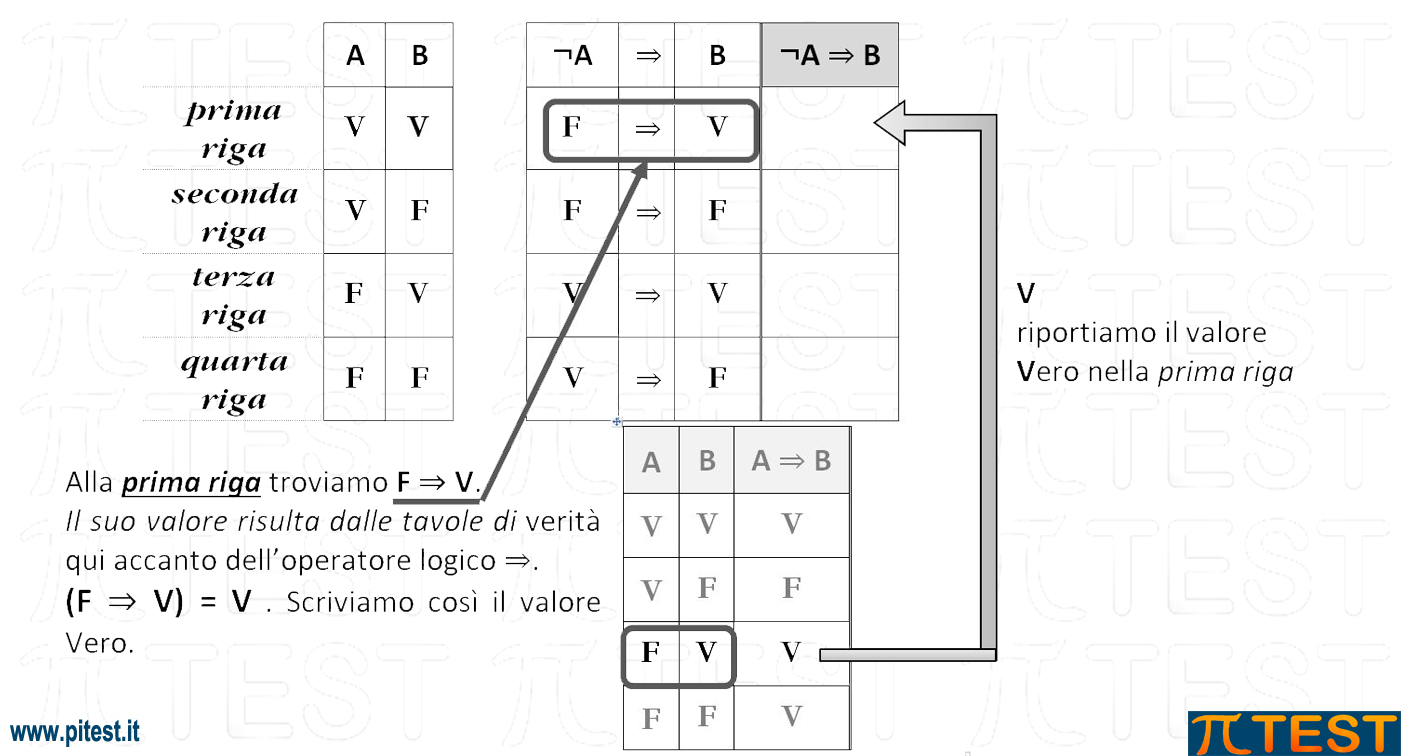
Facciamo attenzione a non confonderci nella lettura di A e B. Nella tavola qui a fianco (Tavola di verità dell’opera dell’operatore logico ⇒). A e B sono generici e dobbiamo considerare solo i valori di V e F per ricavare l’applicazione dell’operatore logico ⇒.
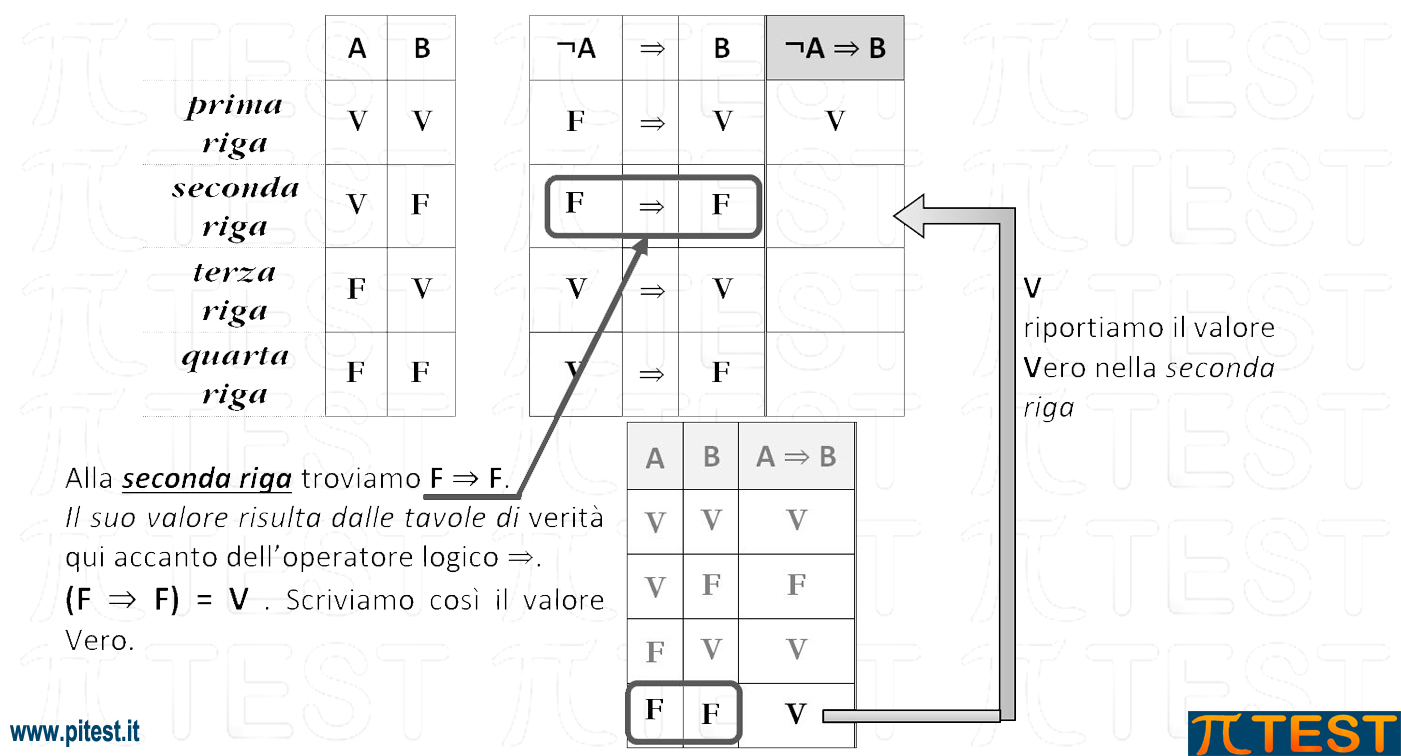
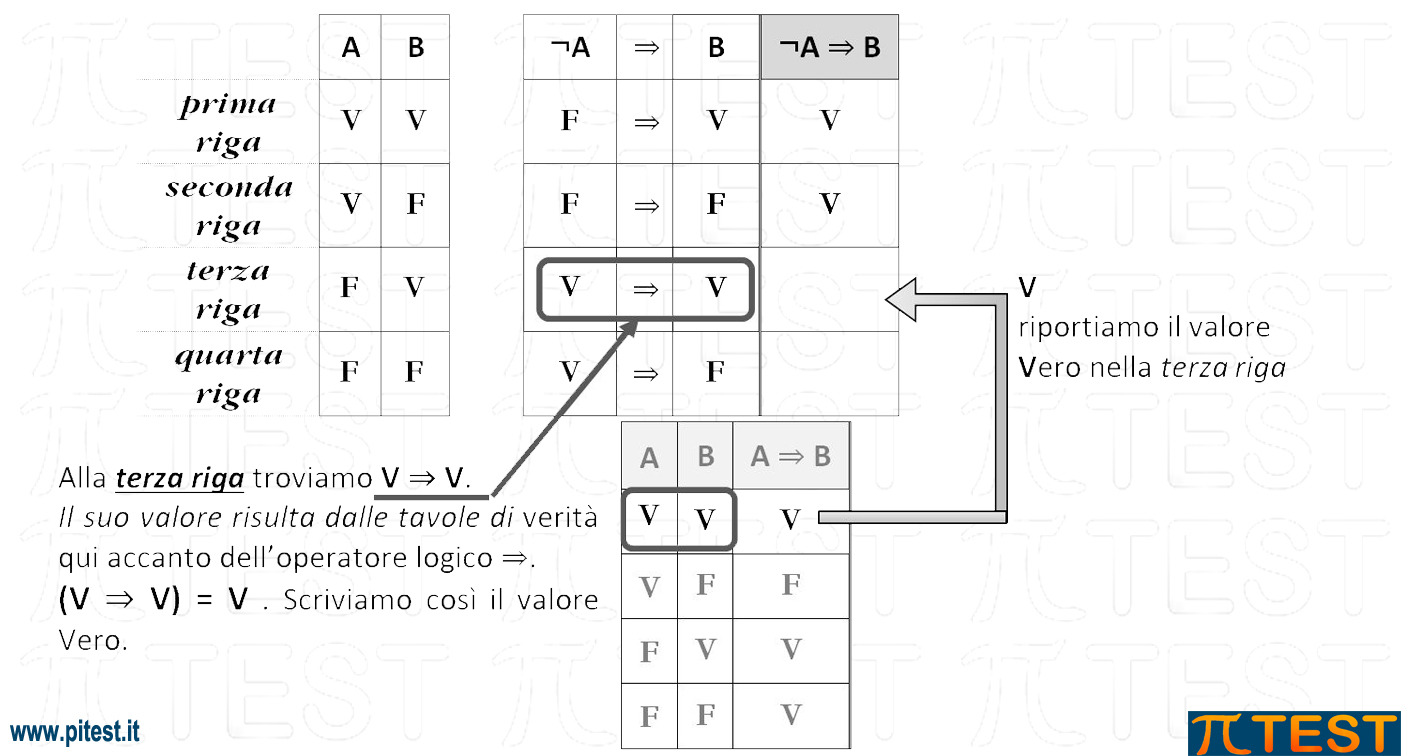
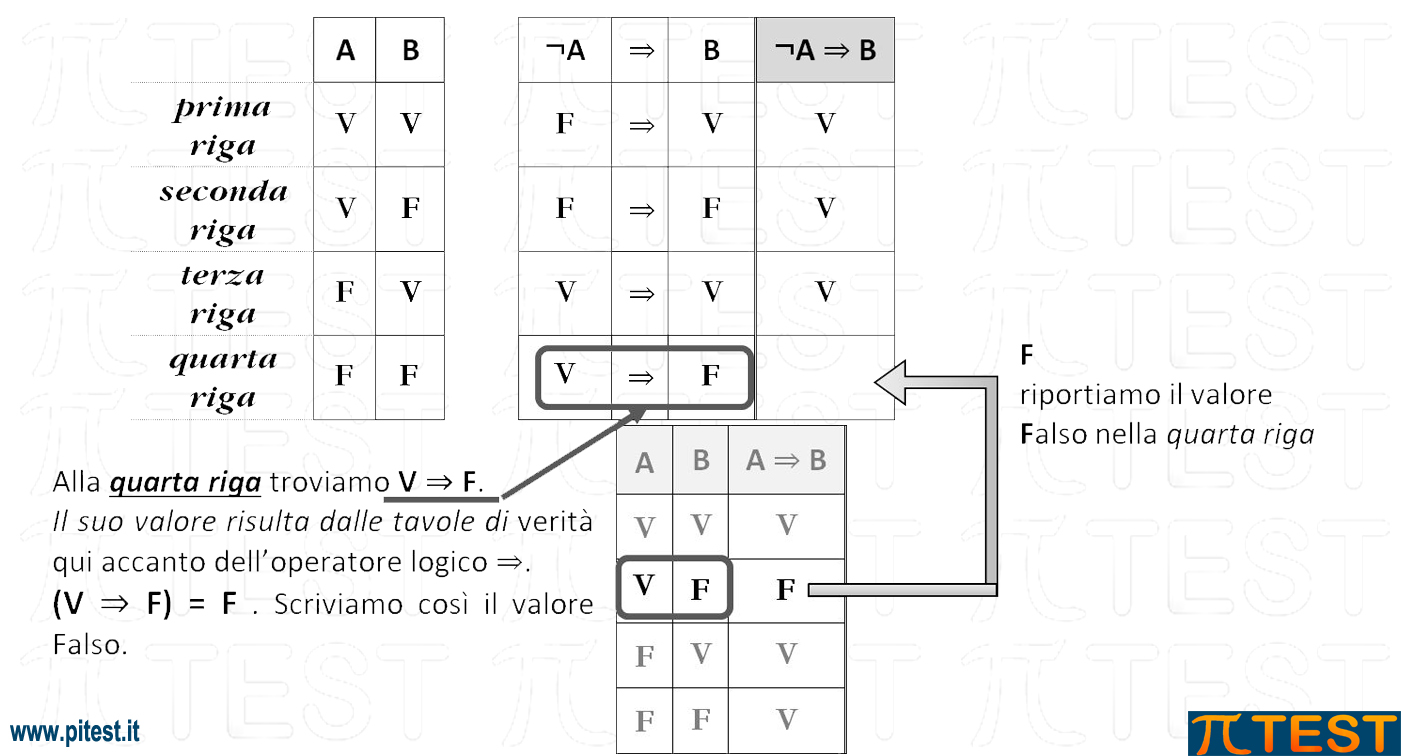
Abbiamo costruito così la tavola di verità di ¬A ⇒ B
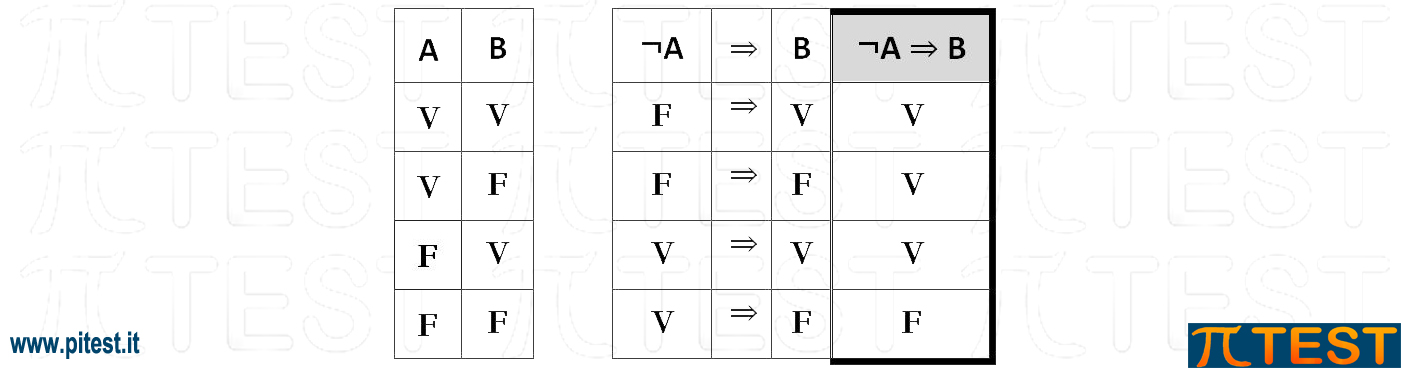
Possiamo ora proseguire per costruire la tavola di verità della proposizione del quiz (¬A ⇒ B) ˄ A
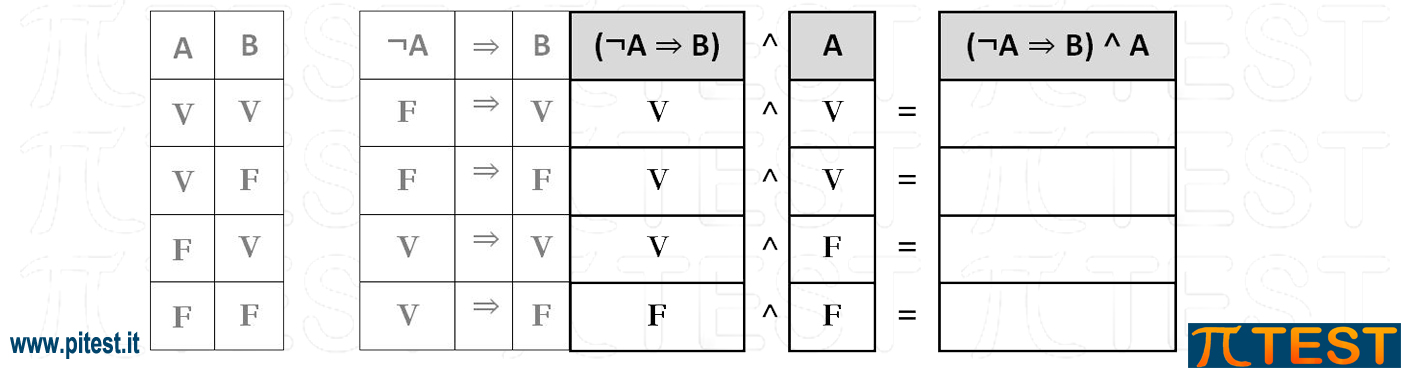
Per completare la tavola bisogna effettuare l’operazione AND (˄) tra le due colonne (¬A ⇒ B) e A.
Possiamo far riferimento alla tavola di verità dell’operatore logico AND (˄) indicata nel test del quiz.
Avremo così alla prima riga e alla seconda riga V ˄ V = V
Alla terza riga V ˄ F = F
Alla quarta riga F ˄ F = F
Compiliamo così la tavola:
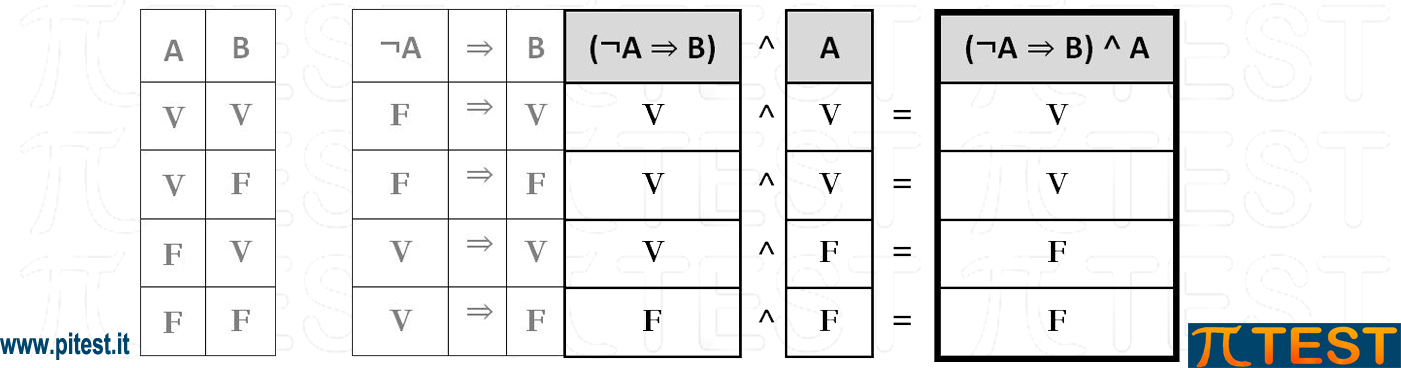
La risposta corretta è la D)


