Prima di valutare le risposte in questo tipo di quiz è bene considerare i due casi limite: il caso di massima concentrazione (tutti i cellulari di un solo ragazzo) e di massima equidistribuzione (tutti i ragazzi con lo stesso numero di cellulari, o quasi). Queste due situazioni limite possono essere utili nella valutazione rapida delle risposte.

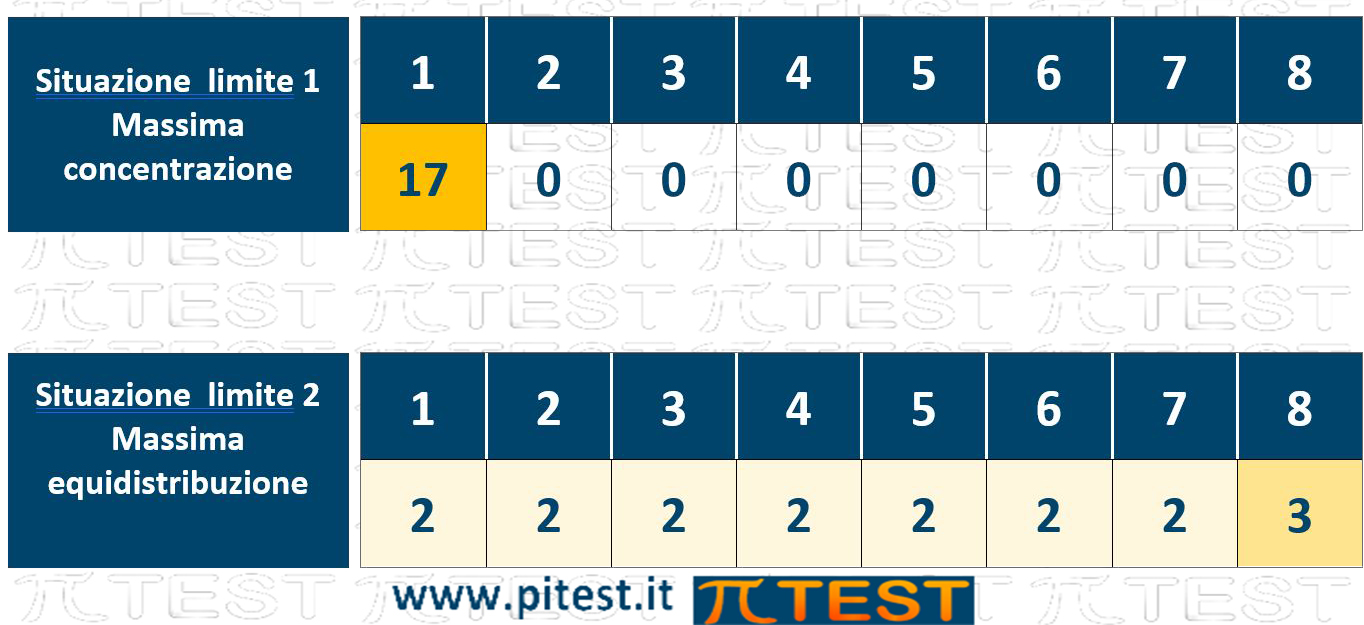
Analizziamo le risposte. Osserviamo che troviamo affermazioni nette che, per essere vere, devono essere vere in qualsiasi situazione. Basta trovare una situazione nella quale una affermazione non sia valida per poter dire che tale affermazione non è sicuramente vera.

A)  C'è un unico ragazzo che possiede almeno 3 cellulari.

È facile individuare una situazione nella quale esistono due (o anche più) ragazzi che possiedono più di tre cellulari ciascuno.

Tale situazione contrasta con quanto affermato nella risposta A) che non è corretta.

B)  Almeno un ragazzo possiede esattamente 3 cellulari

Nella situazione limite 1 troviamo la negazione di quanto affermato bella risposta B). In tale situazione nessuno possiede esattamente 3 cellulari.

C) Nessun ragazzo possiede più di 3 cellulari

Nella situazione limite 1 troviamo la negazione di quanto affermato bella risposta C). In tale situazione ce ne è uno che ne possiede 17 (più di tre).

D) Almeno un ragazzo possiede almeno 3 cellulari

Per negare questa affermazione dovremmo avere che tutti i ragazzi possiedono al massimo 2 cellulari. Così facendo però la somma dei cellulari è al massimo 16. I cellulari sono invece 17. Perciò dopo aver assegnato 2 cellulari a ciascun ragazzo ci troviamo costretti ad assegnare il diciassetesimo cellulare ad un ragazzo realizzando la situazione limite 2. L'affermazione D) è perciò corretta. 

E) C'è un unico ragazzo che possiede esattamente 3 cellulari

Nella situazione limite 1 troviamo la negazione di quanto affermato bella risposta E). In tale situazione nessuno possiede esattamente tre cellulari.