Se cinque muratori costruiscono un muro di cinta lungo 4 metri in mezz’ora, quanti muratori sarebbero teoricamente necessari per costruirne uno della stessa altezza e della stessa larghezza, ma lungo 40 metri, in 9000 secondi?
Come si può vedere nello studio dei problemi di produzione con persone che hanno lo stesso ritmo di lavoro, gestiamo i dati in una tabella a tre colonne nelle quali collochiamo le tre variabili del problema: numero di lavoratori, quantità di prodotto e tempo impiegato.
Prima di iniziare la tecnica risolutiva, osserviamo che il quiz non specifica esplicitamente che i muratori sono tutti equivalenti e possiedono lo stesso ritmo di lavoro. L’equivalenza dei lavoratori però risulta facilmente immaginabile in quanto non viene specificato nulla a proposito.
L’oggetto della produzione è un muro la cui unica variabile quantificabile è la lunghezza in quanto altezza e larghezza sono uniformi.
Impostiamo la tabella con i dati del quiz. Trasformiamo i secondi in minuti per avere dati omogenei (9000 secondi = 9000/60 = 150 minuti)

Osserviamo che varia sia la quantità di prodotto che il tempo. Non possiamo perciò applicare un calcolo immediato. Dobbiamo suddividere il problema in due trasformazioni successive da calcolare separatamente. Introduciamo una riga intermedia nella tabella nel seguente modo:

Abbiamo due grandezze che variano: il prodotto cha varia da 4 a 40 ed il tempo che varia da 30 a 150.
In un primo passaggio, che rappresenteremo nella riga intermedia, manteniamo costante uno dei due parametri a nostra scelta e variamo l’altro. In questo modo potremo effettuare i calcoli nelle modalità che abbiamo visto. Ad Esempio manteniamo inizialmente costante il tempo al valore iniziale e variamo il prodotto da 4 a 40.

Effettuiamo il calcolo considerando solo le prime due righe:
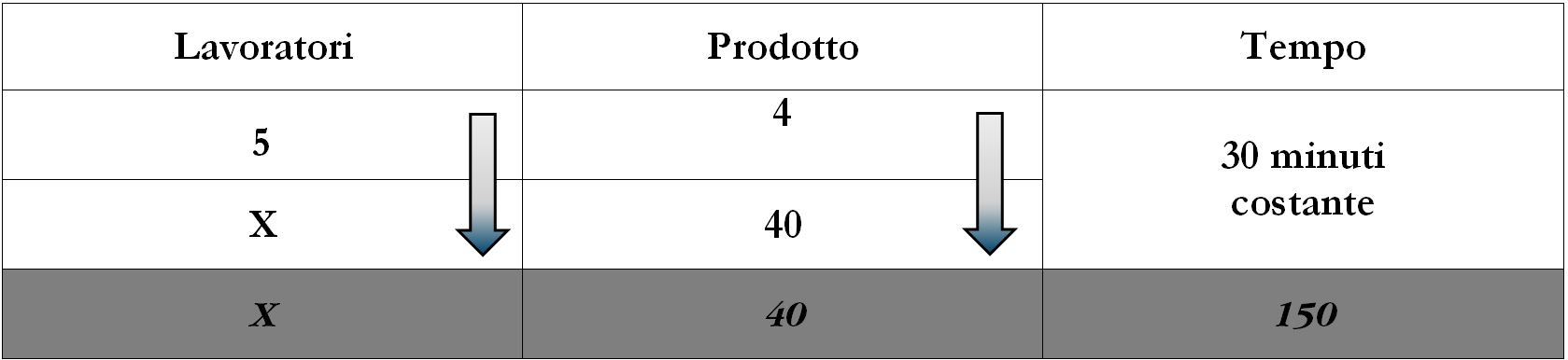
Abbiamo il tempo di produzione costante e proporzionalità diretta tra lavoratori e produzione.
5 : X = 4 : 40
X = (5 • 40) / 4 = 50
Possiamo giungere allo stesso risultato con questo ragionamento: se la lunghezza si decuplica (da 4 a 40 c’è un fattore x10), allora, per la proporzionalità diretta, si moltiplica per 10 anche il prodotto e perciò avremo:
5 • 10 = 50
Trascriviamo questo risultato intermedio nella tabella e passiamo ad occuparci del secondo passaggio.
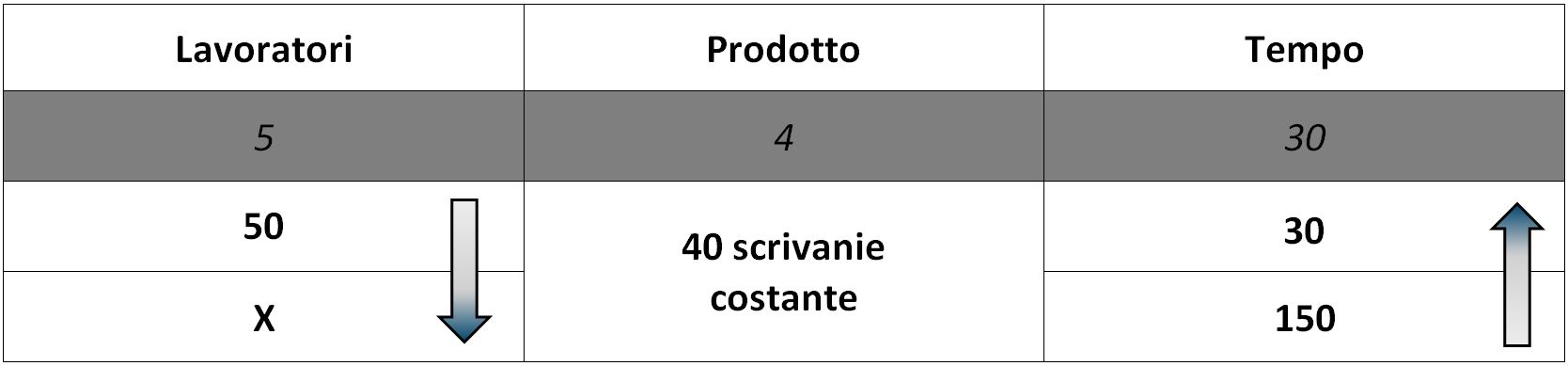
Abbiamo la produzione costante e proporzionalità inversa tra lavoratori e tempo.
50 : X = 150 : 30
X = (50 • 30) /150 = 10
Possiamo giungere allo stesso risultato con questo ragionamento: se il tempo quintuplica (da 30 a 150 c’è un fattore x5), allora, per la proporzionalità inversa, si divide per 5 il numero dei lavoratori e perciò avremo 50:5=10.
La risposta corretta è la E)


