È stato commesso un furto in una banca e sono stati arrestati tre sospetti: Fabio, Dario ed Enrico.
L'inquirente sa che due di essi dicono la verità e uno solo mente. Fabio dice che è stato Dario a commettere il furto, Enrico proclama la propria innocenza, così come Dario. In base alle precedenti informazioni si può essere sicuri che il colpevole:
Impostiamo una tabella con tre colonne per i tre sospetti ed indichiamo con segni grafici le affermazioni dei tre. Notiamo che nei quiz illustrati negli esempi precedenti trovavamo regole fornite dal quiz stesso. Invece nel presente quiz abbiamo affermazioni delle tre persone, affermazioni che possono essere vere o false Prepariamo perciò una tabella nel modo seguente. Indicheremo con “sì” il fatto di essere colpevole e “no” il fatto di non esserlo.
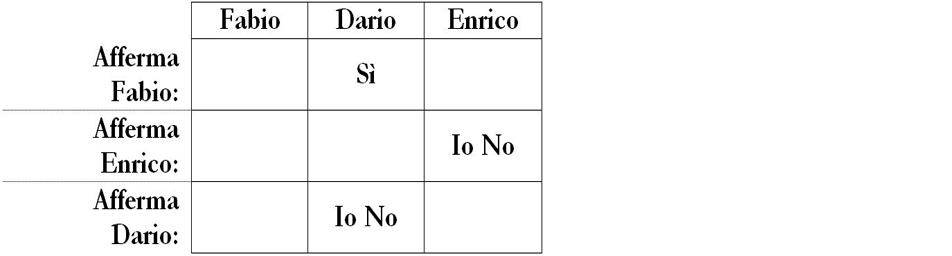
Dobbiamo ora impostare ragionamenti sul fatto che “due di essi dicono la verità e uno solo mente”.
Sviluppiamo tutti i casi possibili.
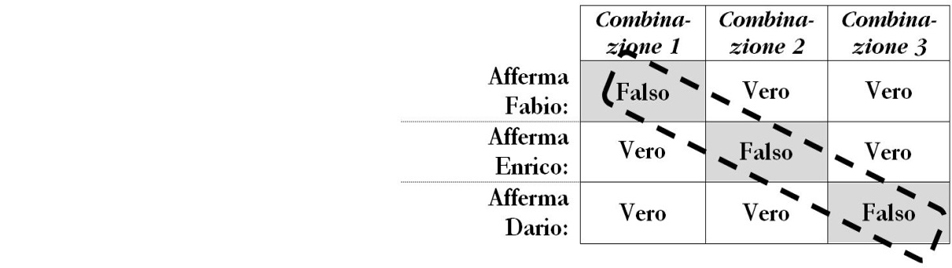
Piazziamo “Falso” nella prima, poi nella seconda ed infine nella terza colonna e posizioniamo ”Vero” nelle rimanenti celle. Questo metodo di costruire la tabella serve a non dimenticare nessun caso
Per ciascuna combinazione andiamo a valutare se ne deriva una situazione di contraddizione o di congruenza che ci possa dare indicazioni per l’individuazione del colpevole.
Estendiamo la tabella delle affermazioni aggiungendo a destra tre colonne delle tre possibili combinazioni Vero-Falso. In basso aggiungeremo tre righe per riportare le conclusioni che potremo trarre relativamente alle tre combinazioni Vero-Falso.
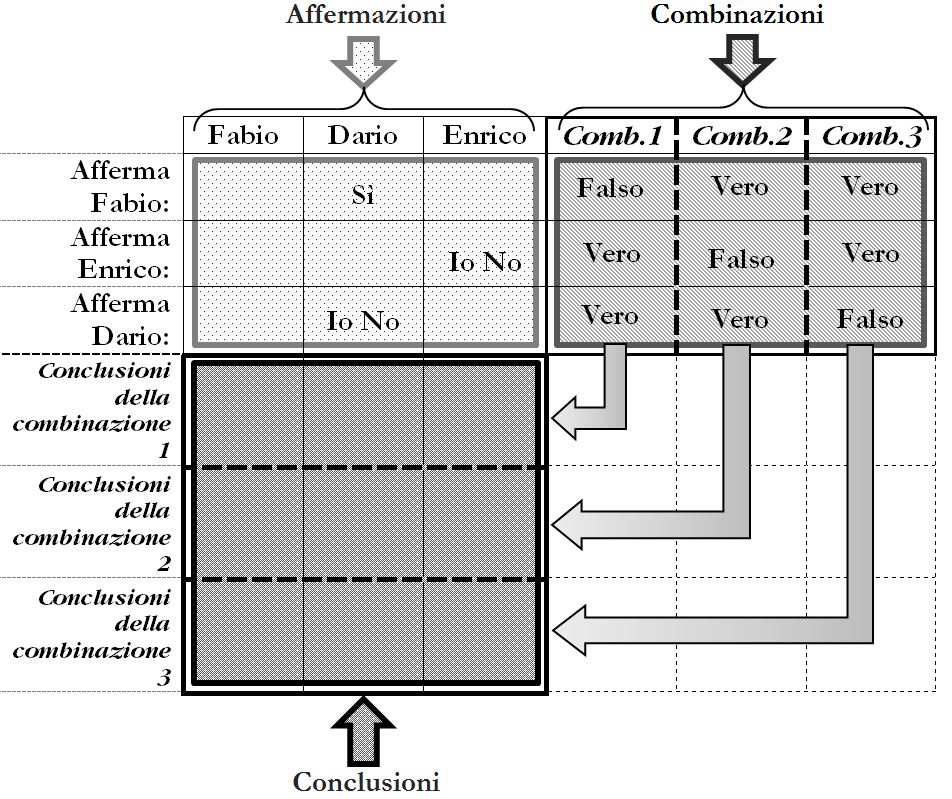
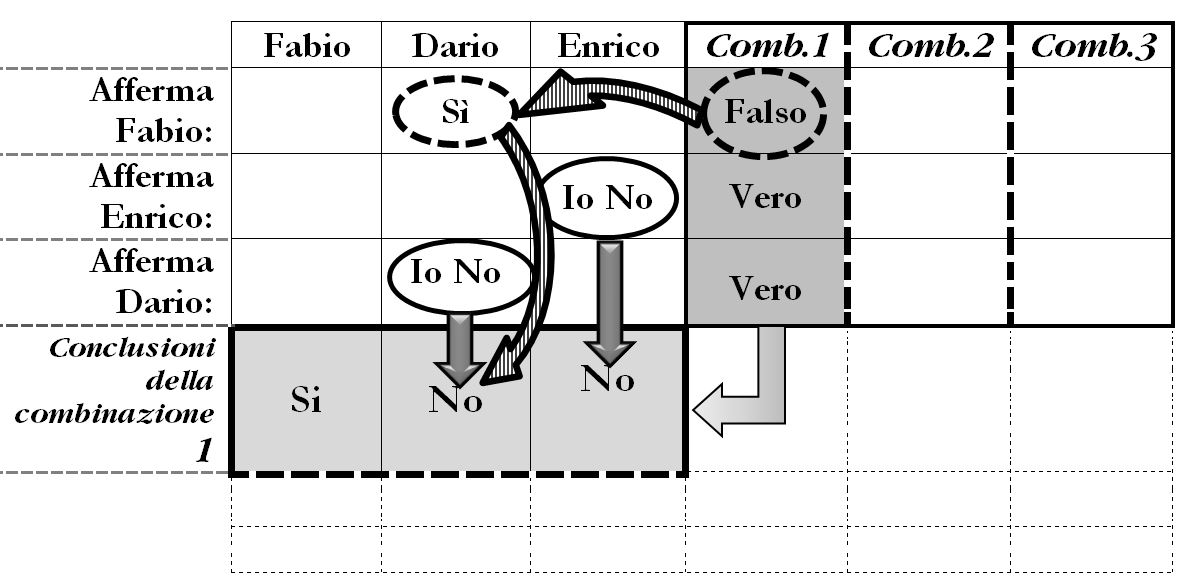
Valutiamo la prima combinazione Falso – Vero – Vero (Fabio falso, Enrico vero e Dario vero).
L’affermazione di Fabio sulla colpevolezza di Dario è falsa e di conseguenza Dario è innocente. Questo è congruente con il fatto che Dario, che dice il vero, proclama di essere innocente. L’affermazione di Enrico è vera e pertanto è innocente. Risultano così innocenti Dario ed Enrico e di conseguenza poiché ci deve essere almeno un colpevole, il colpevole è Fabio.
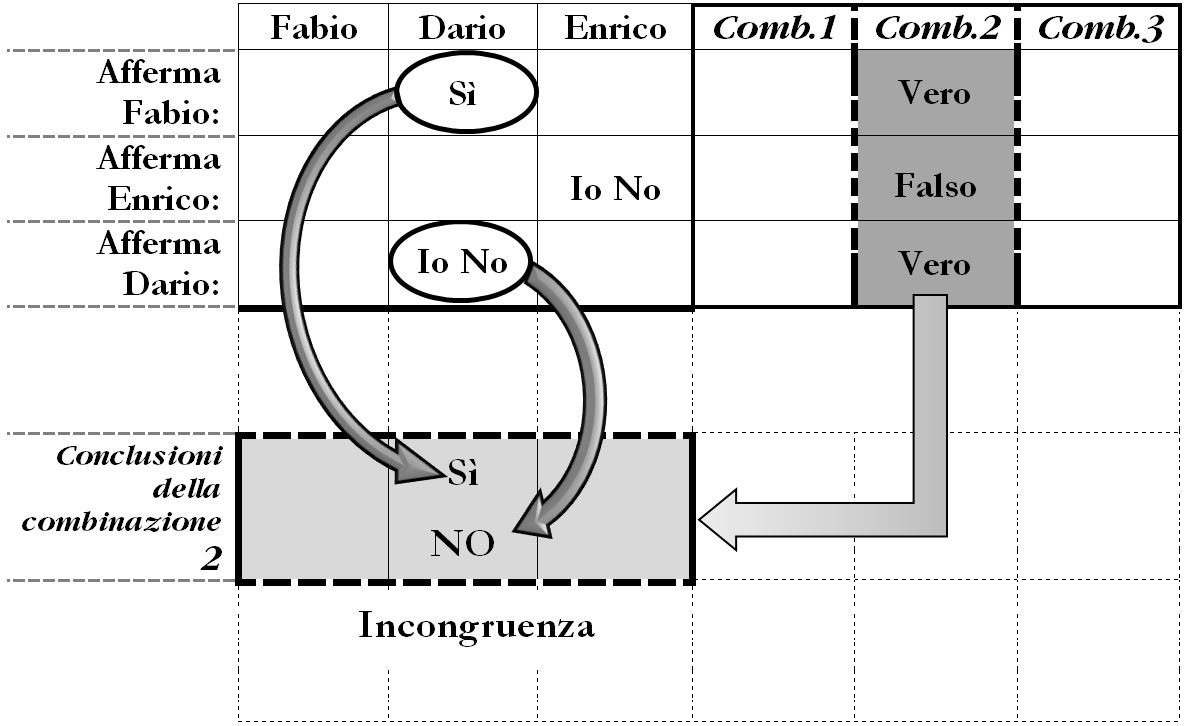
Valutiamo la seconda combinazione Vero – Falso – Vero (Fabio vero, Enrico falso e Dario vero).
L’affermazione che Fabio fa sulla colpevolezza di Dario è vera e di conseguenza Dario è colpevole. Questo non è congruente con il fatto che Dario, che dice il vero, afferma di non essere colpevole. Questa situazione di incongruenza rende NON VALIDA la combinazione “Vero – Falso – Vero”. Possiamo già scartare la seconda combinazione e non ci curiamo di svilupparla ulteriormente, cioè non andiamo a valutare l’effetto dell’affermazione di Enrico.
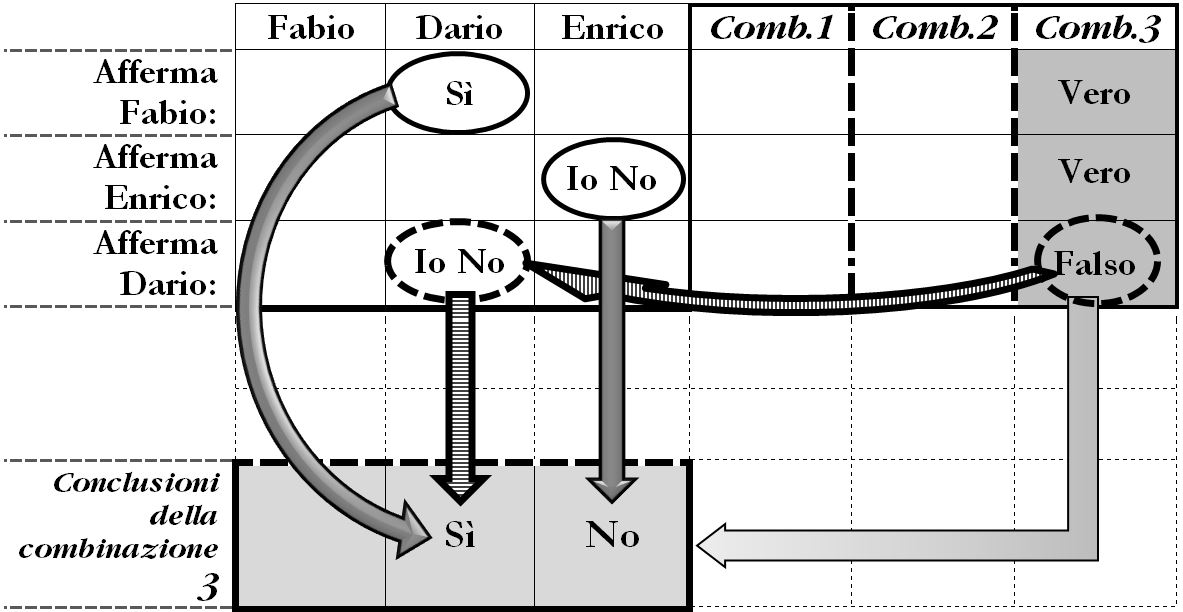
Valutiamo la terza combinazione Vero – Vero – Falso (Fabio vero, Enrico vero e Dario falso).
L’affermazione che Fabio fa sulla colpevolezza di Dario è vera e di conseguenza Dario è colpevole. Questo è congruente con la dichiarazione (falsa) che Dario dice di se stesso. L’affermazione di Enrico è vera e pertanto è innocente. Risultano così Che Dario è colpevole ed Enrico è innocente. Non possiamo dire nulla a proposito di Fabio.
Rivediamo l’insieme delle conclusioni che derivano dalle tre combinazioni.
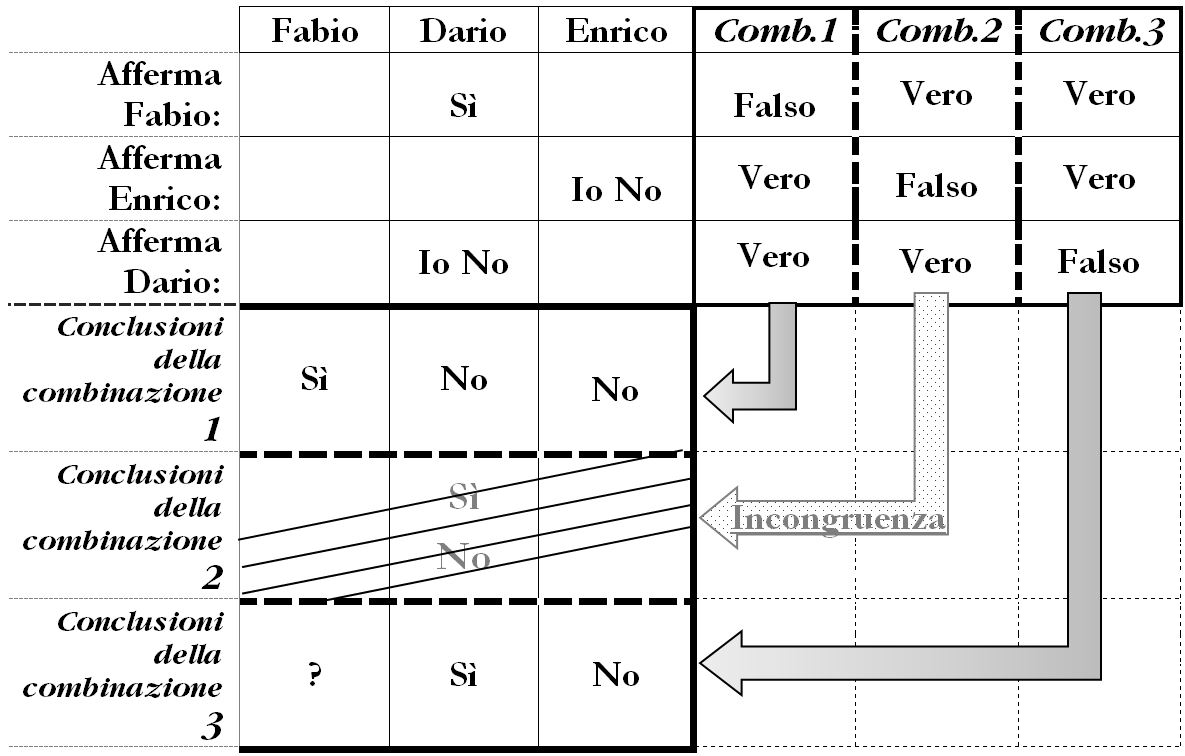
La prima e la terza combinazione risultano coerenti e le deduzioni che ne derivano sono perciò possibili. Invece la seconda combinazione non è accettabile per incongruenza. L’unica affermazione certa che possiamo fare su questo quadro di possibili deduzioni è che Enrico in ogni caso risulta innocente.
La risposta corretta è la E)
| ASSOCIAZIONE – INDICAZIONI DIRETTE | ||||
| QUIZ 1 | QUIZ 2 | QUIZ 3 | QUIZ 4 | QUIZ 5 |
| ASSOCIAZIONE – SOLUZIONE PER CONGRUENZA E CONTRADDIZIONE | ||
| QUIZ 6 | QUIZ 7 | QUIZ 8 |
© il testo è di esclusiva proprietà dell’autore ed è sottoposto a COPYRIGHT – non è consentito alcun utilizzo diverso dallo studio gratuito degli utenti del sito


